练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．${[（1-\sqrt{2}）{\;}^2]^{\frac{1}{2}}}$=$\sqrt{2}$-1．

    分析 利用根式的运算性质即可得出．

    解答 解：原式=$（\sqrt{2}-1）^{2×\frac{1}{2}}$=$\sqrt{2}$-1．
    故答案为：$\sqrt{2}$-1．

    点评 本题考查了根式的运算性质，考查了计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．计算：
    （1）计算27${\;}^{\frac{2}{3}}$-2${\;}^{lo{g}_{2}3}$×log2$\frac{1}{8}$+log23×log34；
    （2）已知0＜x＜1，x+x-1=3，求x${\;}^{\frac{1}{2}}$-x${\;}^{-\frac{1}{2}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=x|x+m|-4，m∈R
    （1）若g（x）=f（x）+4为奇函数，求实数m的值；
    （2）当m=-3时，求函数f（x）在x∈[2，4]上的值域；
    （3）若f（x）＜0对x∈（0，1]恒成立，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．函数y=f（x）的定义域是（-1，1），则函数f（2x-1）的定义域为（　　）
    A．（0，1）B．（-1，1）C．（-3，1）D．（-1，0）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．函数f（x）=sin（2x+$\frac{π}{6}$），则函数f（x）的图象（　　）
    A．关于点（$\frac{5π}{12}$，0）对称B．关于点（$\frac{π}{2}$，0）对称
    C．关于直线x=$\frac{5π}{12}$对称D．关于直线x=$\frac{π}{12}$对称

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

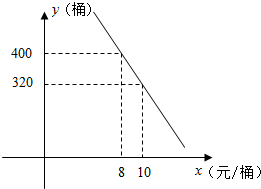    17．高一某班共有学生43人，据统计原来每人每年用于购买饮料的平均支出是120元．若该班全体学生改饮某品牌的桶装纯净水，经测算和市场调查，其年总费用由两部分组成，一部分是购买纯净水的费用，另一部分是其它费用260元，其中，纯净水的销售价x（元/桶）与年购买总量y（桶）之间满足如图直线所示关系．
    （1）求y关于x的函数关系式，并写出函数的定义域；
    （2）若该班每年需要纯净水360桶，请你根据提供的信息比较，该班全体学生改饮桶装纯净水的年总费用与该班全体学生购买饮料的年总费用，哪一个更少？说明你的理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．下列命题中正确的个数是（　　）
    ①过异面直线a，b外一点P有且只有一个平面与a，b都平行；
    ②异面直线a，b在平面α内的射影相互垂直，则a⊥b；
    ③底面是等边三角形，侧面都是等腰三角形的三棱锥是正三棱锥；
    ④直线a，b分别在平面α，β内，且a⊥b，则α⊥β．
    A．0B．1C．2D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知幂函数f（x）=xα的图象过点（8，4），则α=$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数$f（x）=2{cos^2}x+sin（{\frac{7π}{6}-2x}）-1（{x∈R}）$．
    （1）求函数f（x）的周期及单调递增区间；
    （2）在△ABC中，三内角A，B，C的对边分别为a，b，c，已知函数f（x）的图象经过点$（{A，\frac{1}{2}}）$，若b+c=2a，且$\overrightarrow{AB}•\overrightarrow{AC}$=6，求a的值．

    查看答案和解析>>

    同步练习册答案