
【题目】已知函数f(x)=x3﹣3x;
(1)求f(x)的单调区间;
(2)求f(x)在区间[﹣3,2]上的最值.
【答案】
(1)解:∵f(x)=x3﹣3x,
∴f'(x)=3x2﹣3=3(x+1)(x﹣1).
令 f'(x)=0,得x=﹣1,x=1.
若 x∈(﹣∞,﹣1)∪(1,+∞),则f'(x)>0,
故f(x)在(﹣∞,﹣1)上是增函数,f(x)在(1,+∞)上是增函数,
若 x∈(﹣1,1),则f'(x)<0,
故f(x)在(﹣1,1)上是减函数;
(2)解:∵f(﹣3)=﹣18,f(﹣1)=2,f(1)=﹣2,f(2)=2,
∴当x=﹣3时,f(x)在区间[﹣3,2]取到最小值为﹣18.
∴当x=﹣1或2时,f(x)在区间[﹣3,2]取到最大值为2.
【解析】(1)先求出函数f(x)=x3﹣3x的导函数f′(x),分别令f′(x)>0和f′(x)<0便可求出函数f(x)的单调区间;(2)分别求出两个短点f(﹣3)和f(2)的值以及极值f(﹣1)和f(1)的值,比较一下便可求出f(x)在区间[﹣3,2]上的最大值和最小值.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查 结果如下表所示:
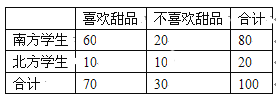
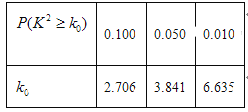
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
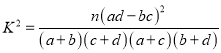 ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个班级某次考试的数学成绩(单位:分),从甲、乙两个班级中分别随机抽取5名学生的成绩作样本,如图是样本的茎叶图,规定:成绩不低于120分时为优秀成绩. 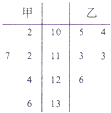
(1)从甲班的样本中有放回的随机抽取2个数据,求其中只有一个优秀成绩的概率;
(2)从甲、乙两个班级的样本中分别抽取2名学生的成绩,记获优秀成绩的总人数为X,求X的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地建一座桥,两端的桥墩已建好,这两墩相距m米,余下的工程只需要建两端桥墩之间的桥面和桥墩.经预测一个桥墩的工程费用为256万元,距离为x米的相邻两墩之间的桥面工程费用为(2+ ![]() )x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
)x万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为y万元.假设需要新建n个桥墩.
(1)写出n关于x的函数关系式;
(2)写出y关于x的函数关系式;
(3)当m=640米时,需新建多少个桥墩才能使y最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在各棱长均为2的三棱柱ABC﹣A1B1C1中,侧面A1ACC1⊥底面ABC,且∠A1AC= ![]() ,点O为AC的中点.
,点O为AC的中点. 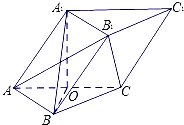
(1)求证:AC⊥平面A1OB;
(2)求二面角B1﹣AC﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com