
【题目】已知函数f(x)=ex-m(x+1)+1(m∈R).
(1)若函数f(x)的极小值为1,求实数m的值;
(2)当x≥0时,不等式![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】(1)m=1;(2)(-∞,2]
【解析】
(1)求得![]() ,分类讨论求得函数的单调性,即可求解函数的极值;
,分类讨论求得函数的单调性,即可求解函数的极值;
(2)令![]() ,求得
,求得![]() ,令
,令![]() ,得
,得![]() ,再
,再![]() ,利用导数得到
,利用导数得到![]() 的单调性与最值,即可求解.
的单调性与最值,即可求解.
(1)由题意,函数![]() ,则
,则![]() ,
,
①若m≤0,则f'(x)>0,∴f(x)在(-∞,+∞)单调递增,所以f(x)无极值,
②若m>0,当x>lnm时,f'(x)>0,
当x<lnm时,f'(x)<0,f(x)在(-∞,lnm)单调递减,在(lnm,+∞)单调递增,
所以f(x)的极小值为f(lnm),由m-m(lnm+1)+1=1,解得m=1.
(2)令![]() (x≥0),
(x≥0),![]() ,
,
令![]() ,
,![]() ,
,
令![]() ,
,
显然p(x)在[0,+∞)单调递增,∴p(x)![]() p(0)=2-m.
p(0)=2-m.
①当m![]() 2时,p(x)
2时,p(x)![]() 0,∴h'(x)
0,∴h'(x)![]() 0,∴h(x)在[0,+∞)单调递增,
0,∴h(x)在[0,+∞)单调递增,
∴![]() ,即g'(x)
,即g'(x)![]() 0,∴g(x)在[0,+∞)单调递增,
0,∴g(x)在[0,+∞)单调递增,
所以g(x)![]() g(0)=2-m
g(0)=2-m![]() 0,此时符合题意;
0,此时符合题意;
②当m![]() 2时,p(0)<0,∴x0∈(0,+∞),使p(x0)=0,
2时,p(0)<0,∴x0∈(0,+∞),使p(x0)=0,
故p(x)在(0,x0)恒为负值,h(x)在(0,x0)单调递减,此时![]() ,
,
所以g(x)在(0,x0)单调递减,所以g(x)![]() g(0)=2-m
g(0)=2-m![]() 0,此时不符合题意,
0,此时不符合题意,
故所求m的取值范围为(-∞,2].


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】设点A是抛物线![]() 上到直线
上到直线![]() 的距离最短的点,点B是抛物线上异于点A的一点,直线AB与l交于P,过点P作y轴的平行线交抛物线于点C.
的距离最短的点,点B是抛物线上异于点A的一点,直线AB与l交于P,过点P作y轴的平行线交抛物线于点C.
(1)求点A的坐标;
(2)求证:直线BC过定点;
(3)求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校从参加高二年级期末考试的学生中抽出一些学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),所得数据整理后,列出了如下频率分布表.
分组 | 频数 | 频率 |
[40,50) | A | 0.04 |
[50,60) | 4 | 0.08 |
[60,70) | 20 | 0.40 |
[70,80) | 15 | 0.30 |
[80,90) | 7 | B |
[90,100] | 2 | 0.04 |
合计 | C | 1 |

(1)在给出的样本频率分布表中,求A,B,C的值;
(2)补全频率分布直方图,并利用它估计全体高二年级学生期末数学成绩的众数、中位数;
(3)现从分数在[80,90),[90,100]的9名同学中随机抽取两名同学,求被抽取的两名学生分数均不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E、F分别为PC的三等分点.
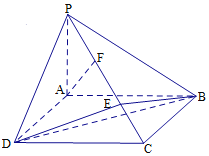
(1)证明:AF∥平面EBD;
(2)已知AP=AD=1,AB=2,求二面角E-BD-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是离心率为
是离心率为![]() 的椭圆的左、右顶点,
的椭圆的左、右顶点,![]() ,
,![]() 是该椭圆的左、右焦点,
是该椭圆的左、右焦点,![]() ,
,![]() 是直线
是直线![]() 上两个动点,连接
上两个动点,连接![]() 和
和![]() ,它们分别与椭圆交于点
,它们分别与椭圆交于点![]() ,
,![]() 两点,且线段
两点,且线段![]() 恰好过椭圆的左焦点
恰好过椭圆的左焦点![]() .当
.当![]() 时,点
时,点![]() 恰为线段
恰为线段![]() 的中点.
的中点.
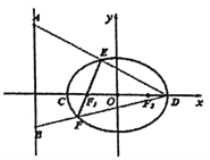
(1)求椭圆的方程;
(Ⅱ)判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 位置关系,并加以证明.
位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线C1的普通方程为![]() ,曲线C2参数方程为
,曲线C2参数方程为![]() 为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为
为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,直线l的极坐标方程为![]() .
.
(1)求C1的参数方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)已知P是C2上参数![]() 对应的点,Q为C1上的点,求PQ中点M到直线
对应的点,Q为C1上的点,求PQ中点M到直线![]() 的距离取得最大值时,点Q的直角坐标.
的距离取得最大值时,点Q的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校从参加高二年级期末考试的学生中抽出一些学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),所得数据整理后,列出了如下频率分布表.
分组 | 频数 | 频率 |
[40,50) | A | 0.04 |
[50,60) | 4 | 0.08 |
[60,70) | 20 | 0.40 |
[70,80) | 15 | 0.30 |
[80,90) | 7 | B |
[90,100] | 2 | 0.04 |
合计 | C | 1 |
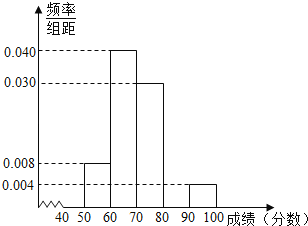
(1)在给出的样本频率分布表中,求A,B,C的值;
(2)补全频率分布直方图,并利用它估计全体高二年级学生期末数学成绩的众数、中位数;
(3)现从分数在[80,90),[90,100]的9名同学中随机抽取两名同学,求被抽取的两名学生分数均不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,(其中
,(其中![]() 是自然对数的底数).
是自然对数的底数).
(1)若![]() ,求函数
,求函数![]() 在
在![]() 上的最大值.
上的最大值.
(2)若![]() ,关于x的方程
,关于x的方程![]() 有且仅有一个根,求实数k的取值范围.
有且仅有一个根,求实数k的取值范围.
(3)若对任意的![]() 、
、![]() ,
,![]() ,不等式
,不等式![]() 都成立,求实数a的取值范围.
都成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com