
【题目】如图,一个![]() 的矩形
的矩形![]() (
(![]() ),被截取一角(即
),被截取一角(即![]() ),
),![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() .
.
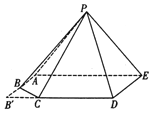
(1)证明: ![]() ;
;
(2)求二面角![]() 的大小的余弦值.
的大小的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)过![]() 作
作![]() ,由面面垂直性质定理得
,由面面垂直性质定理得![]() 平面
平面![]() ,即得
,即得![]() ,再在平面
,再在平面![]() 内,根据平几知识计算可得
内,根据平几知识计算可得![]() .最后根据线面垂直判定定理得
.最后根据线面垂直判定定理得![]() 平面
平面![]() ,即得
,即得![]() .(2)求二面角,一般利用空间向量进行求解,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,利用向量数量积求法向量夹角,最后根据二面角与向量夹角之间关系求解.
.(2)求二面角,一般利用空间向量进行求解,先根据条件建立空间直角坐标系,设立各点坐标,利用方程组解出各面法向量,利用向量数量积求法向量夹角,最后根据二面角与向量夹角之间关系求解.
试题解析:(Ⅰ)证明:因为![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
所以截去的![]() 是等腰直角三角形.
是等腰直角三角形.
如图,过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
因为![]() ,所以
,所以![]() ,
, ![]() .
.
![]() ,故
,故![]() 是等腰直角三角形,所以
是等腰直角三角形,所以![]() ,
,
所以![]() ,即
,即![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,而
,而![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅱ)解:如图4,以![]() 为原点,
为原点, ![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,

则![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
所以![]() ,
, ![]() ,
, ![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
由 得
得
所以平面![]() 的一个法向量为
的一个法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
由 得
得
所以平面![]() 的一个法向量为
的一个法向量为![]() ,
,
所以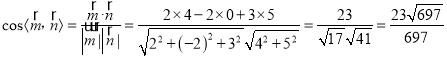 ,
,
因为二面角![]() 为钝二面角,
为钝二面角,
所以二面角![]() 的大小的余弦值为
的大小的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知直线l过点A(﹣3,4)
(1)若l与直线y=﹣2x+5平行,求其一般式方程;
(2)若l与直线y=﹣2x+5垂直,求其一般式方程;
(3)若l与两个坐标轴的截距之和等于12,求其一般式方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市计划销售某种产品,先试销该产品![]() 天,对这
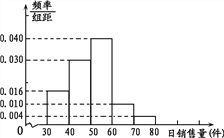
天,对这![]() 天日销售量进行统计,得到频率分布直方图如图.
天日销售量进行统计,得到频率分布直方图如图.
(Ⅰ)若已知销售量低于50的天数为23,求![]() ;
;
(Ⅱ)厂家对该超市销售这种产品的日返利方案为:每天固定返利45元,另外每销售一件产品,返利3元;频率估计为概率.依此方案,估计日返利额的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地政府为了对房地产市场进行调控决策,统计部门对外来人口和当地人口进行了买房的心理预期调研,用简单随机抽样的方法抽取了110人进行统计,得到如下列联表(不全):
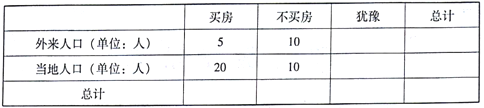
已知样本中外来人口数与当地人口数之比为3:8.
(1)补全上述列联表;
(2)从参与调研的外来人口中用分层抽样方法抽取6人,进一步统计外来人口的某项收入指标,若一个买房人的指标记为3,一个犹豫人的指标记为2,一个不买房人的指标记为1,现在从这6人中再随机选取3人,用![]() 表示这3人指标之和,求
表示这3人指标之和,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形
(Ⅰ)若AC⊥BC,证明:直线BC⊥平面ACC1A1;
(Ⅱ)设D、E分别是线段BC、CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.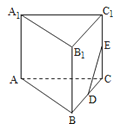
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣(a+1)x+1(a∈R)
(1)若关于x的不等式f(x)>0的解集为R,求实数a的取值范围;
(2)若关于x的不等式f(x)≤0的解集为P,集合Q={x|0≤x≤1},若P∩Q=,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com