
����Ŀ������лƺ�̲��ij��2010����2016���˾������루��λ����Ԫ�����������±���
��� | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
��ݴ���x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
�˾�������y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
������y����x�����Իع鷽�̣�
�������ã����еĻع鷽�̣�����2010����2016��ô��˾�������ı仯�������Ԥ��ô�2017���˾������룮
�����ع�ֱ�ߵ�б�ʺͽؾ����С�˷����ƹ�ʽ�ֱ�Ϊ�� ![]() =
=  ��
�� ![]() =
= ![]() ��
�� ![]() ��
��
���𰸡��⣺����������������������ƽ���� ![]() =
= ![]() =4��
=4�� ![]() =
= ![]() =4.3��
=4.3��
�� ![]() ��xi��
��xi�� ![]() ����yi��
����yi�� ![]() ��=����3��������1.4��+����2��������1��+����1��������0.7��+0+1��0.5+2��0.9+3��1.6=14
��=����3��������1.4��+����2��������1��+����1��������0.7��+0+1��0.5+2��0.9+3��1.6=14
![]() ��xi��
��xi�� ![]() ��2=9+4+4+0+1+4+9=28��
��2=9+4+4+0+1+4+9=28��
�� ![]() =
= 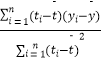 =
= ![]()
�� ![]() =4.3��
=4.3�� ![]() ��4=2.3��
��4=2.3��
��y����x�����Իع鷽��Ϊ��y= ![]() x+2.3��
x+2.3��
�����ɣ��ɵ����Իع鷽��Ϊy= ![]() x+2.3��
x+2.3��
2017���˾������룬��x=8���ɵ�y= ![]() ����Ԫ����
����Ԫ����
��Ԥ��ô�2017���˾�������Ϊ6.3��Ԫ��
���������������ù�ʽ���![]() ��
��![]() ���Ӷ��ɵ�y����x�����Իع鷽�̣��������ã�I�������Իع鷽�̣����� x=8���ɵøô�2017���˾������룮
���Ӷ��ɵ�y����x�����Իع鷽�̣��������ã�I�������Իع鷽�̣����� x=8���ɵøô�2017���˾������룮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ԲE�� ![]() ��a��b��0�����㣨
��a��b��0�����㣨 ![]() ��1��������ֱ��
��1��������ֱ�� ![]() x+2y��4=0���У�
x+2y��4=0����
��1������ԲE�ķ��̣�
��2������ԲE��x�ύ��M��N���㣬��ԲE�ڲ��Ķ���Pʹ|PM|��|PO|��|PN|�ɵȱ����У��� ![]()
![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ���ѧ�������������ڼ���ѧ�е��о���������1ǧ�꣬�ڡ������������У����ĸ����Ϊֱ�������ε��������Ϊ��Ğ����֪ij����Ğ��������ͼ��ͼ��ʾ����ñ�Ğ�������ı����Ϊ�� �� 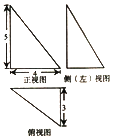
A.200��
B.50��
C.100��
D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʱ��3��10�գ�CBA�����������7��4ʤ�ƣ���ij��ȡʤ�ij�������ֹ���α���������ý�������ʸ�����2��3��2�����̣��������������½���������һ��������������½��ӳ�����ռ�ţ�����ʱӵ���������ƣ��½�������������Ȼ�������ͳ������������������������ܾ������̣�
���� | ������ | ���� | �ͳ� | ����ʱ�� | �����ص� |
17��3��10�� | �½������� | �½� | ���� | 20��00 | ��³ľ�� |
17��3��12�� | �½������� | �½� | ���� | 20��00 | ��³ľ�� |
17��3��15�� | �������½� | ���� | �½� | 20��00 | ��Ϫ |
17��3��17�� | �������½� | ���� | �½� | 20��00 | ��Ϫ |
17��3��19�� | �������½� | ���� | �½� | 20��00 | ��Ϫ |
17��3��22�� | �½������� | �½� | ���� | 20��00 | ��³ľ�� |
17��3��24�� | �½������� | �½� | ���� | 20��00 | ��³ľ�� |
��1���������������ƣ�ÿ����������ʤ�ĸ��ʾ�Ϊ ![]() ���ͳ�ȡʤ�ĸ��ʾ�Ϊ
���ͳ�ȡʤ�ĸ��ʾ�Ϊ ![]() �����������Աȷ�4��1��ʤ�ĸ��ʣ�
�����������Աȷ�4��1��ʤ�ĸ��ʣ�
��2��������������ͳ�ƣ�ÿ��������֯�߿ɻ����Ʊ����50��Ԫ�������ͳ��أ��������������ͳ����أ�ÿ����ÿ��������ʤ�ĸ��ʾ�Ϊ ![]() ���豾�ΰ�����У�ֻ��������֧�ӣ���֯������õ���Ʊ����ΪX����X�ķֲ��м���ѧ������
���豾�ΰ�����У�ֻ��������֧�ӣ���֯������õ���Ʊ����ΪX����X�ķֲ��м���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���ԭ��OΪ���㣬x���������Ϊ���ᣬ����������ϵ������C1�IJ�������Ϊ ![]() ����Ϊ������������ C2�ļ����귽��Ϊ��cos�ȩ�
����Ϊ������������ C2�ļ����귽��Ϊ��cos�ȩ� ![]() ��sin�ȩ�4=0��
��sin�ȩ�4=0��
��1��������C1����ͨ���̺����� C2��ֱ�����귽�̣�
��2����PΪ����C1��һ�㣬QΪ���� C2��һ�㣬��|PQ|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����С������Ϊ
����С������Ϊ![]() ���ҵ�
���ҵ�![]() ʱ��
ʱ�� ![]() ȡ�����ֵ
ȡ�����ֵ![]() .
.
��1����![]() �Ľ���ʽ�����������䣻
�Ľ���ʽ�����������䣻
��2����![]() ����
����![]() ����
����![]() ;
;
��3��������![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ��
��![]() ������λ���Ⱥ�õ�����
������λ���Ⱥ�õ�����![]() ��ż��������
��ż��������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵĺ���f��x��=ex+mx2��m��m��0������x1+x2=1ʱ������ʽf��x1��+f��0����f��x2��+f��1�����������ʵ��x1��ȡֵ��Χ�ǣ� ��
A.�����ޣ�0��
B.![]()
C.![]()
D.��1��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=xlnx+ax��a��R��
��1����a=1ʱ��������y=f��x���ڵ㣨1��f��1�����������߷��̣�
��2������x��1��f��x������b+a��1��x��b�������������b�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ΪԲ�ĵ�Բ��
ΪԲ�ĵ�Բ��![]() �ύ��
�ύ��![]() ��
��![]() �ύ��
�ύ��![]() ������
������![]() Ϊԭ��.
Ϊԭ��.
��1����֤��![]() �����Ϊ��ֵ��
�����Ϊ��ֵ��
��2����ֱ��![]() ��Բ
��Բ![]() ���ڵ�
���ڵ�![]() ����
����![]() ����Բ
����Բ![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com