
如图所示,已知在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求:

(1)设f(x)为绳子最短长度的平方,求f(x)表达式;
(2)绳子最短时,顶点到绳子的最短距离;
(3)f(x)的最大值.
(1)f(x)=AM2=x2+16(0≤x≤4)(2)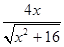 (3)32
(3)32
【解析】
试题分析:将圆锥的侧面沿SA展开在平面上,如图,则该展开图为扇形,且弧AA′的长度L就是⊙O的周长,
∴L=2πr=2π.∴∠ASA′=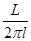 ×360°=
×360°=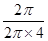 ×360°=90°,
×360°=90°,
(1)由题意知,绳长的最小值为展开图中的AM,其值为AM=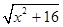 (0≤x≤4),
(0≤x≤4),
∴f(x)=AM2=x2+16(0≤x≤4).
(2)绳子最短时,在展开图中作SR⊥AM,垂足为R,则SR的长度为顶点S到绳子的最短距离.在△SAM中,∵S△SAM=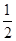 SA·SM=
SA·SM=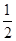 AM· SR,
AM· SR,
∴SR=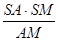 =
=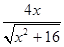 (0≤x≤4).
(0≤x≤4).
(3)∵f(x)=x2+16(0≤x≤4)是增函数,∴f(x)的最大值为f(4)=32.
考点:本小题主要考查扇形的弧长、面积公式等的应用,考查学生的运算求解能力.
点评:解决此类问题的关键是正确转化,将所要求解的问题转化为熟悉的数学问题进行解决.


科目:高中数学 来源: 题型:
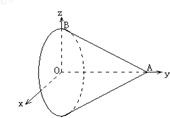 如图所示,Rt△AOB绕直角边AO所在直线旋转一周形成一个圆锥,已知在空间直角坐标系O-xyz中,点B(2,0,0)和点E(0,2,-1)均在圆锥的母线上,则圆锥的体积为
如图所示,Rt△AOB绕直角边AO所在直线旋转一周形成一个圆锥,已知在空间直角坐标系O-xyz中,点B(2,0,0)和点E(0,2,-1)均在圆锥的母线上,则圆锥的体积为
查看答案和解析>>
科目:高中数学 来源: 题型:044
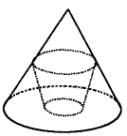
如图所示,已知圆锥的底面半径为R,高为H,在其中有一个高为x,下底面半径与上底面半径之比为λ(0<λ<1)的内接圆台.试问:当x为何值时,圆台的体积最大?并求出这个最大的体积.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com