
【题目】在如图所示的几何体中,四边形![]() 是菱形,
是菱形,![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.

(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(1)详见解析;(2)![]()
【解析】
![]() 利用
利用![]() 与
与![]() 交于
交于![]() ,连接
,连接![]() .证明
.证明![]() ,通过直线与平面平行的判定定理证明
,通过直线与平面平行的判定定理证明![]() 平面
平面![]() ;
;
![]() 对于存在性问题,可先假设存在,即假设
对于存在性问题,可先假设存在,即假设![]() 在线段
在线段![]() 上是否存在点
上是否存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() .再通过建立空间直角坐标系,求出相关点的坐标,利用坐标法进行求解判断.
.再通过建立空间直角坐标系,求出相关点的坐标,利用坐标法进行求解判断.
![]() 与
与![]() 交于
交于![]() ,连接
,连接![]() .
.
由已知可得四边形![]() 是平行四边形,
是平行四边形,
所以![]() 是
是![]() 的中点.
的中点.
因为![]() 是
是![]() 的中点,
的中点,
所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
![]() 由于四边形
由于四边形![]() 是菱形,
是菱形,![]() ,
,![]() 是
是![]() 的中点,可得
的中点,可得![]() .
.
又四边形![]() 是矩形,面
是矩形,面![]() 面
面![]() ,
,
![]() 面
面![]() ,
,
如图建立空间直角坐标系![]() ,
,
则![]() ,0,
,0,![]() ,
,![]() ,0,
,0,![]() ,
,![]() ,2,
,2,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,![]() ,
,![]() .
.
则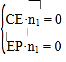 ,
,![]()
![]() ,
,
令![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,
又平面![]() 的法向量
的法向量![]() ,0,
,0,![]() ,
,
![]() ,
,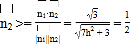 ,解得
,解得![]() ,
,
![]()
![]() ,
,
![]() 在线段
在线段![]() 上不存在点
上不存在点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() .
.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知点![]() ,动点
,动点![]() 到直线
到直线![]() :
:![]() 的距离为
的距离为![]() ,且
,且![]() ,设动点
,设动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)过点![]() 作互相垂直的两条直线,分别交曲线
作互相垂直的两条直线,分别交曲线![]() 于点
于点![]() ,
,![]() 和
和![]() ,
,![]() ,若四边形
,若四边形![]() 面积为
面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() (
(![]() ,
,![]() 是虚数单位),
是虚数单位),![]() ,定义:
,定义:![]() ,
,![]() ,给出下列命题:
,给出下列命题:
①对任意![]() ,都有
,都有![]() ;
;
②若![]() 是复数
是复数![]() 的共轭复数,则
的共轭复数,则![]() 恒成立;
恒成立;
③![]() ,则
,则![]() ;
;
④对任意![]() ,结论
,结论![]() 恒成立;
恒成立;
则其中真命题是( )
A.①②③④B.②③④C.②④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过焦点且垂直于
.过焦点且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 相交所得的弦长为3,直线
相交所得的弦长为3,直线![]() 与椭圆
与椭圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,使得
两点,使得![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由!
的取值范围;若不存在,请说明理由!
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次体育兴趣小组的聚会中,要安排6人的座位,使他们在如图所示的6个椅子中就坐,且相邻座位(如1与2,2与3)上的人要有共同的体育兴趣爱好.现已知这6人的体育兴趣爱好如下表所示,且小林坐在1号位置上,则4号位置上坐的是
小林 | 小方 | 小马 | 小张 | 小李 | 小周 | |
体育兴趣爱好 | 篮球,网球,羽毛球 | 足球,排球,跆拳道 | 篮球,棒球,乒乓球 | 击剑,网球,足球 | 棒球,排球,羽毛球 | 跆拳道,击剑,自行车 |

A.小方B.小张C.小周D.小马
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2002年在北京召开的国际数学家大会的会标是以我国古代数学家的弦图为基础设计的.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图).设其中直角三角形中较小的锐角为![]() ,且
,且![]() ,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
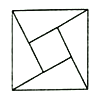
A. 350B. 300C. 250D. 200
查看答案和解析>>
科目:高中数学 来源: 题型:
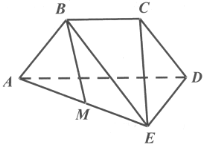
【题目】如图等腰梯形![]() 中
中![]() ,且平面
,且平面 ![]() 平面
平面![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求证:平面 ![]() 平面
平面![]() ;
;
(3)若二面角![]() 的大小为
的大小为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正切值.
所成角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com