
【题目】定义在[﹣3,3]上的增函数f(x)满足f(﹣x)=﹣f(x),且f(m+1)+f(2m﹣1)>0,求实数m的范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2sinx,1),
=(2sinx,1), ![]() =(cosx,1﹣cos2x),函数f(x)=
=(cosx,1﹣cos2x),函数f(x)= ![]()
![]() (x∈R).
(x∈R).
(1)求函数f(x)的最小正周期、最大值和最小值;
(2)求函数f(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光明超市某种商品11月份(30天,11月1日为第一天)的销售价格P(单位:元)与时间t(单位:天,其中)组成有序实数对(t,P),点(t,P)落在如图所示的线段上.该商品日销售量Q(单位:件)与时间t(单位:天,其中t∈N)满足一次函数关系,Q与t的部分数据如表所示.
第t天 | 10 | 17 | 21 | 30 |
Q(件) | 180 | 152 | 136 | 100 |
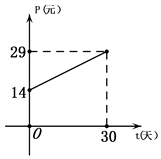
(1)根据图象写出销售价格与时间t的函数关系式P=f(t).
(2)请根据表中数据写出日销售量Q与时间t的函数关系式Q=g(t).
(3)设日销售额为M(单位:元),请求出这30天中第几日M最大,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各小题中,p是q的充分不必要条件的是( ) ①p:m<﹣2或m>6,q:y=x2+mx+m+3有两个零点;
② ![]() ,q:y=f(x)是偶函数;
,q:y=f(x)是偶函数;
③p:cosα=cosβ,q:tanα=tanβ;
④p:A∩B=A,q:(UB)(UA)
A.①②
B.②③
C.③④
D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1C1C是边长为4的正方形.平面ABC⊥平面AA1C1C,AB=3,BC=5. (Ⅰ)求证:AA1⊥平面ABC;
(Ⅱ)求证二面角A1﹣BC1﹣B1的余弦值;
(Ⅲ)证明:在线段BC1上存在点D,使得AD⊥A1B,并求 ![]() 的值.
的值.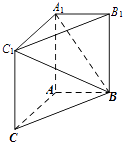
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线y 2=﹣8x的焦点,O为原点,点P是抛物线准线上一动点,点A在抛物线上,且|AF|=4,则|PA|+|PO|的最小值为( )
A.6
B.![]()
C.![]()
D.4+2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且当x>0时,f(x)=lg ![]() ,若对任意实数t∈[
,若对任意实数t∈[ ![]() ,2],都有f(t+a)﹣f(t﹣1)≥0恒成立,则实数a的取值范围 .
,2],都有f(t+a)﹣f(t﹣1)≥0恒成立,则实数a的取值范围 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 在
在 ![]() 上有最大值1和最小值0,设
上有最大值1和最小值0,设 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)若不等式 ![]() 在
在 ![]() 上有解,求实数
上有解,求实数 ![]() 的取值范围;
的取值范围;
(3)若方程 ![]() (
( ![]() 为自然对数的底数)有三个不同的实数解,求实数
为自然对数的底数)有三个不同的实数解,求实数 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com