
| A. | $({-∞,-\frac{3}{2}})$ | B. | $({-∞,-\frac{3}{4}})$ | C. | $({-\frac{3}{4},+∞})$ | D. | $({-\frac{3}{2},+∞})$ |
分析 根据圆的性质,得直线x=ky-1与直线y=x垂直且圆心C(-$\frac{k}{2}$,-$\frac{m}{2}$)在直线y=x上,由此解出k=m=-1,从而得到直线和圆的方程,再由圆心C到直线的距离小于半径,利用点到直线的距离公式即可算出实数p的取值范围.
解答 解:∵直线x=ky-1与圆C相交,且两个交点关于直线y=x对称,
∴圆心C(-$\frac{k}{2}$,-$\frac{m}{2}$)在直线y=x上,可得m=k
∵直线x=ky-1与直线y=x垂直,∴k=m=-1
得直线方程x=-y-1即x+y+1=0,
圆C:x2+y2-x-y+p=0,圆心C($\frac{1}{2}$,$\frac{1}{2}$),半径R=$\sqrt{\frac{1}{2}-p}$
∵直线x+y+1=0与圆C相交,
∴$\frac{|\frac{1}{2}+\frac{1}{2}+1|}{\sqrt{2}}$<$\sqrt{\frac{1}{2}-p}$,解之得p<-$\frac{3}{2}$,
即实数p的取值范围是(-∞,-$\frac{3}{2}$).
故选A.
点评 本题给出直线与圆相交且交点关于直线y=x对称,求参数p的取值范围,着重考查了点到直线的距离公式、直线与圆的方程、直线与圆的位置关系等知识,属于中档题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
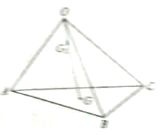
| A. | $\overrightarrow{O{G_1}}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ | B. | $\overrightarrow{O{G_1}}=\frac{1}{9}\overrightarrow{OA}+\frac{1}{9}\overrightarrow{OB}+\frac{1}{9}\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{O{G_1}}=\frac{1}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$ | D. | $\overrightarrow{O{G_1}}=\frac{3}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}+\frac{3}{4}\overrightarrow{OC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
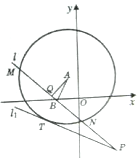 已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.
已知以A(-1,2)点为圆心的圆与直线${l_1}:\frac{1}{2}x+y+\frac{7}{2}=0$相切.过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{5}$ | D. | $\frac{\sqrt{5}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com