练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，已知.

    (1)求角C的值；

    (2)若c＝2，且△ABC的面积为，求a，b.

    【答案】（1） （2）a＝b＝2

    【解析】

    （1）首先利用降次公式、三角形的内角和定理、两角和的余弦公式化简已知条件，得到，由此求得的值.（2）利用三角形的面积公式和余弦定理列方程组，解方程组可求得的值.

    解：(1)2cos2＋(cosB－sinB)cosC＝1，故cosA＋cosBcosC－sinBcosC＝0，

    则－cos(B＋C)＋cosBcosC－sinBcosC＝0，

    展开得：sinBsinC－sinBcosC＝0，

    ∵sinB≠0，即tanC＝，∵C∈(0，π)，C＝.

    (2)三角形面积为absin＝，故ab＝4.

    由余弦定理得4＝(a＋b)2－2ab－ab，所以a＋b＝4，

    故a＝b＝2.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，甲、乙两个企业的用电负荷量关于投产持续时间（单位：小时）的关系均近似地满足函数.

    （1）根据图象，求函数的解析式；

    （2）为使任意时刻两企业用电负荷量之和不超过9，现采用错峰用电的方式，让企业乙比企业甲推迟小时投产，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求不等式的解集；

    （2）若不等式对任意的恒成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题：实数满足，：实数满足

    （1）若为真命题，求实数的取值范围.

    （2）若是的充分不必要条件，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设奇函数在（0，+∞）上为单调递增函数，且，则不等式的解集为 。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知一个几何体是由一个直角三角形绕其斜边旋转一周所形成的．若该三角形的周长为12米，三边长由小到大依次为a，b，c，且b恰好为a，c的算术平均数．

    （1）求a，b，c；

    （2）若在该几何体的表面涂上一层油漆，且每平方米油漆的造价为5元，求所涂的油漆的价格．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱台中，平面ABCD，四边形ABCD为平行四边形，，，，，E为DC中点．

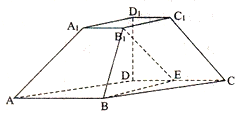
    （1）求证：平面；

    （2）求证：；

    （3）求三棱锥的高．

    （注：棱台的两底面相似）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某商场有奖销售中，购满100元商品得1张奖券，多购多得，100张奖券为一个开奖单位，每个开奖单位设特等奖1个，一等奖10个，二等奖50个，设一张奖券中特等奖、一等奖、二等奖的事件分别为A，B，C，可知其概率平分别为．

    （1）求1张奖券中奖的概率；

    （2）求1张奖券不中特等奖且不中一等奖的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系xOy中，抛物线y2=4x的焦点为F，抛物线上有三个动点A,B,C.

    （1）若，求；

    （2）若，AB的垂直平分线经过一个定点Q，求△QAB面积的最大值.

    查看答案和解析>>

    同步练习册答案