
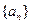 各项均为正数,其前
各项均为正数,其前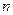 项和
项和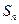 满足
满足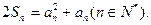
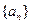 为等差数列
为等差数列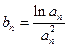 ,记
,记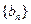 的前
的前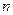 项和为
项和为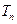 ,求证:
,求证: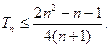
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源:不详 题型:解答题
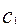 ,
,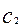 ...,
...,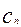 ,...是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线y=
,...是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线y=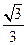 x相切,对每一个正整数n,圆
x相切,对每一个正整数n,圆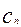 都与圆
都与圆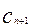 相互外切,以
相互外切,以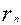 表示
表示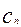 的半径,已知
的半径,已知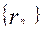 为递增数列.
为递增数列.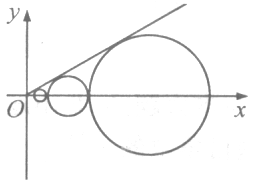
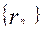 为等比数列;
为等比数列;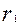 =1,求数列错误!不能通过编辑域代码创建对象。的前n项和.
=1,求数列错误!不能通过编辑域代码创建对象。的前n项和.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
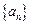 的通项公式为
的通项公式为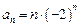 ,则数列
,则数列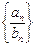 成等比数列是数列
成等比数列是数列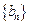 的通项公式为
的通项公式为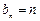 的( ▲ )
的( ▲ )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.m(1+r)6 | B.m(1+r)7 |
C.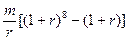 | D.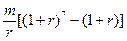 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com