
【题目】已知函数f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是π,若其图象向右平移
)的最小正周期是π,若其图象向右平移 ![]() 个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
个单位后得到的函数为奇函数,则函数y=f(x)的图象( )
A.关于点( ![]() ,0)对称
,0)对称
B.关于直线x= ![]() 对称
对称
C.关于点( ![]() ,0)对称
,0)对称
D.关于直线x= ![]() 对称
对称
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:
【题目】某车间共有![]() 名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.

(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间![]() 名工人中有几名优秀工人;
名工人中有几名优秀工人;
(Ⅲ) 从该车间![]() 名工人中,任取2人,求恰有1名优秀工人的概率.
名工人中,任取2人,求恰有1名优秀工人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的焦点
的焦点![]() 、
、![]() 在
在![]() 轴上,且椭圆
轴上,且椭圆![]() 经过
经过![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 交于点
交于点![]() ,与抛物线
,与抛物线![]() :
: ![]() 交于
交于![]() 、
、![]() 两点,当直线
两点,当直线![]() 过
过![]() 时
时![]() 的周长为
的周长为![]() .
.
(Ⅰ)求![]() 的值和
的值和![]() 的方程;
的方程;
(Ⅱ)以线段![]() 为直径的圆是否经过
为直径的圆是否经过![]() 上一定点,若经过一定点求出定点坐标,否则说明理由。
上一定点,若经过一定点求出定点坐标,否则说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级 | 1 | 2 | 3 | 4 | 5 |
数学( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量![]() ,
, ![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级 | 1 | 2 | 3 | 4 | 5 |
数学( | 111 | 113 | 119 | 125 | 127 |
物理( | 92 | 93 | 96 | 99 | 100 |
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量![]() ,
, ![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:  ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
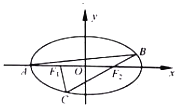
【题目】如图,设点![]() ,
, ![]() ,
, ![]() 分别为椭圆
分别为椭圆![]() 的左顶点和左,右焦点,过点
的左顶点和左,右焦点,过点![]() 作斜率为
作斜率为![]() 的直线交椭圆于另一点
的直线交椭圆于另一点![]() ,连接
,连接![]() 并延长交椭圆于点
并延长交椭圆于点![]() .
.
(1)求点![]() 的坐标(用
的坐标(用![]() 表示);
表示);
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com