
【题目】【2017镇江一模20】已知函数![]() ,
,![]() (
(![]() 为常数).
为常数).
(1)若函数![]() 与函数
与函数![]() 在
在![]() 处有相同的切线,求实数
处有相同的切线,求实数![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,证明:
,证明:![]() ;
;
(3)若对任意![]() ,不等式恒
,不等式恒![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】己知椭圆 ![]() (m>n>0)的离心率e的值为
(m>n>0)的离心率e的值为 ![]() ,右准线方程为x=4.如图所示,椭圆C左右顶点分别为A,B,过右焦点F的直线交椭圆C于M,N,直线AM,MB交于点P.
,右准线方程为x=4.如图所示,椭圆C左右顶点分别为A,B,过右焦点F的直线交椭圆C于M,N,直线AM,MB交于点P. 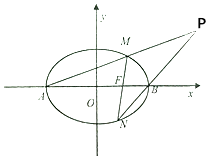
(1)求椭圆的标准方程;
(2)若点P(4, ![]() ),直线AN,BM的斜率分别为k1 , k2 , 求
),直线AN,BM的斜率分别为k1 , k2 , 求 ![]() .
.
(3)求证点P在一条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017安徽阜阳二模】一企业从某生产线上随机抽取![]() 件产品,测量这些产品的某项技术指标值
件产品,测量这些产品的某项技术指标值![]() ,得到的频率分布直方图如图.
,得到的频率分布直方图如图.
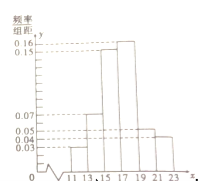
(1)估计该技术指标值![]() 平均数
平均数![]() ;
;
(2)在直方图的技术指标值分组中,以![]() 落入各区间的频率作为
落入各区间的频率作为![]() 取该区间值的频率,若
取该区间值的频率,若![]() ,则产品不合格,现该企业每天从该生产线上随机抽取
,则产品不合格,现该企业每天从该生产线上随机抽取![]() 件产品检测,记不合格产品的个数为
件产品检测,记不合格产品的个数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(1,2),
=(1,2), ![]() =(x,1);
=(x,1);
(1)若( ![]() +2
+2 ![]() )⊥(2
)⊥(2 ![]() ﹣
﹣ ![]() )时,求x的值;
)时,求x的值;
(2)若向量 ![]() 与向量
与向量 ![]() 的夹角为锐角,求x的取值范围.
的夹角为锐角,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,若∠BAC=90°,AB=AC=AA1 , 则异面直线BA1与AC1所成的角等于( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017南京一模19】设函数![]() ,
,![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的方程
的方程![]() (其中
(其中![]() 为自然对数的底数);
为自然对数的底数);
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)当![]() 时,记函数
时,记函数![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式
![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某通讯公司需要在三角形地带OAC区域内建造甲、乙两种通信信号加强中转站,甲中转站建在区域BOC内,乙中转站建在区域AOB内.分界线OB固定,且OB=(1+ ![]() )百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°.设OA=x(3≤x≤6)百米,OC=y百米.
)百米,边界线AC始终过点B,边界线OA、OC满足∠AOC=75°,∠AOB=30°,∠BOC=45°.设OA=x(3≤x≤6)百米,OC=y百米.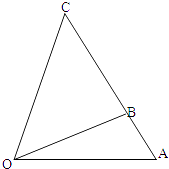
(1)试将y表示成x的函数,并求出函数y的解析式;
(2)当x取何值时?整个中转站的占地面积S△OAC最小,并求出其面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点C(t, ![]() )(t∈R,t≠0)为圆心的圆过原点O.
)(t∈R,t≠0)为圆心的圆过原点O.
(1)设直线3x+y﹣4=0与圆C交于点M、N,若|OM|=|ON|,求圆C的方程;
(2)在(1)的条件下,设B(0,2),且P、Q分别是直线l:x+y+2=0和圆C上的动点,求|PQ|﹣|PB|的最大值及此时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017辽宁鞍山市最后一次模】如图所示,在三棱锥![]() 中,侧面
中,侧面![]() ,
, ![]() 是全等的直角三角形,
是全等的直角三角形, ![]() 是公共的斜边且
是公共的斜边且![]() ,
, ![]() ,另一侧面
,另一侧面![]() 是正三角形.
是正三角形.

(1)求证: ![]() ;
;
(2)若在线段![]() 上存在一点
上存在一点![]() ,使
,使![]() 与平面
与平面![]() 成
成![]() 角,试求二面角
角,试求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com