
【题目】对于函数![]() ,若在其定义域内存在实数
,若在其定义域内存在实数![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 有“※点”
有“※点”![]() 。
。
(1)判断函数![]() 在
在![]() 上是否有“※点”。并说明理由;
上是否有“※点”。并说明理由;
(2)若函数![]() 在
在![]() 上有“※点”,求正实数a的取值范围。
上有“※点”,求正实数a的取值范围。
【答案】(1)见解析;(2)![]()
【解析】
(1)令![]() ,利用零点存在定理,判断端点处的函数值是否异号即可;
,利用零点存在定理,判断端点处的函数值是否异号即可;
(2)若函数在(0,+∞)上有“※点”,只需方程![]() 在该区间上有实根,然后将对数方程化为二次方程,借助于二次函数的性质可以解决.
在该区间上有实根,然后将对数方程化为二次方程,借助于二次函数的性质可以解决.
(1)由题意知,令![]() ,则
,则![]() 为g(x)的零点,因为
为g(x)的零点,因为![]() ,所以
,所以![]() ,由零点存在定理可知,函数
,由零点存在定理可知,函数![]() 在区间
在区间![]() 上至少有1个实根,即
上至少有1个实根,即![]() 至少有1个实根,
至少有1个实根,
所以函数![]() 在
在![]() 上有“※点”。
上有“※点”。
(2)若函数![]() 在
在![]() 上有“※点”,则存在实数
上有“※点”,则存在实数![]() ,使得
,使得![]() 成立,即
成立,即![]() ,
,
整理得![]() ,
,![]() 。
。
当a=2时,![]() ,不合题意
,不合题意
当![]() 时,令
时,令![]() ,则
,则![]() 在
在![]() 上有零点。
上有零点。
当![]() 时,开口向下,对称轴
时,开口向下,对称轴![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,
所以![]() 在
在![]() 上恒小于零,不合题意,当
上恒小于零,不合题意,当![]() 时,开口向上,对称轴
时,开口向上,对称轴![]() ,
,
由题意只要![]() ,即
,即![]() ,解得
,解得![]() 。因为
。因为![]() ,所以
,所以![]() .综上所述:
.综上所述:![]() 。
。


科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 且a2=8,S4=40.数列{bn}的前n项和为Tn , 且Tn﹣2bn+3=0,n∈N* .
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)设cn=![]() , 求数列{cn}的前n项和Pn .
, 求数列{cn}的前n项和Pn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2002年北京国际数学家大会会标,是以中国古代数学家赵爽的弦图为基础而设计的,弦图用四个全等的直角三角形与一个小正方形拼成的一个大正方形![]() 如图
如图![]() ,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为
,若大、小正方形的面积分别为25和1,直角三角形中较大锐角为![]() ,则
,则![]() 等于
等于![]()
![]()

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设椭圆C: ![]() (a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限.
(a>b>0),动直线l与椭圆C只有一个公共点P,且点P在第一象限. 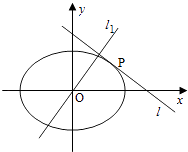
(1)已知直线l的斜率为k,用a,b,k表示点P的坐标;
(2)若过原点O的直线l1与l垂直,证明:点P到直线l1的距离的最大值为a﹣b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面![]() 以任意角度截正方体,所截得的截面图形可以是_____
以任意角度截正方体,所截得的截面图形可以是_____![]() 填上所有你认为正确的序号
填上所有你认为正确的序号![]()
![]() 正三边形
正三边形 ![]() 正四边形
正四边形 ![]() 正五边形
正五边形 ![]() 正六边形
正六边形 ![]() 钝角三角形
钝角三角形 ![]() 等腰梯形
等腰梯形 ![]() 非矩形的平行四边形
非矩形的平行四边形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在充分竞争的市场环境中,产品的定价至关重要,它将影响产品的销量,进而影响生产成本、品牌形象等![]() 某公司根据多年的市场经验,总结得到了其生产的产品A在一个销售季度的销量
某公司根据多年的市场经验,总结得到了其生产的产品A在一个销售季度的销量![]() 单位:万件
单位:万件![]() 与售价
与售价![]() 单位:元
单位:元![]() 之间满足函数关系
之间满足函数关系 ,A的单件成本
,A的单件成本![]() 单位:元
单位:元![]() 与销量y之间满足函数关系
与销量y之间满足函数关系![]() .
.
![]() 当产品A的售价在什么范围内时,能使得其销量不低于5万件?
当产品A的售价在什么范围内时,能使得其销量不低于5万件?
![]() 当产品A的售价为多少时,总利润最大?
当产品A的售价为多少时,总利润最大?![]() 注:总利润
注:总利润![]() 销量
销量![]() 售价
售价![]() 单件成本
单件成本![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin(2x+1)的图象,只需把y=sin2x的图象上所有的点( )
A.向左平行移动 ![]() 个单位长度
个单位长度
B.向右平行移动 ![]() 个单位长度
个单位长度
C.向左平行移动1个单位长度
D.向右平行移动1个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】说明:请同学们在(A)(B)两个小题中任选一题作答.
(A)小明计划搭乘公交车回家,经网上公交实时平台查询,得到838路与611路公交车预计到达公交![]() 站的时间均为8:30,已知公交车实际到达时间与网络报时误差不超过10分钟.
站的时间均为8:30,已知公交车实际到达时间与网络报时误差不超过10分钟.
(1)若小明赶往公交![]() 站搭乘 611 路,预计小明到达
站搭乘 611 路,预计小明到达![]() 站时间在8:20到8:35,求小明比车早到的概率;
站时间在8:20到8:35,求小明比车早到的概率;
(2)求两辆车到达![]() 站时间相差不超过5分钟的概率.
站时间相差不超过5分钟的概率.
(B)小明计划搭乘公交车回家,经网上公交实时平台查询,得到838路与611路公交车预计到达公交![]() 站的之间均为8:30.已知公交车实际到达时间与网络报时误差不超过10分钟
站的之间均为8:30.已知公交车实际到达时间与网络报时误差不超过10分钟
(1)求两辆车到达![]() 站时间相差不超过5分钟的概率
站时间相差不超过5分钟的概率
(2)求838路与611路公交车实际到站时间与网络报时的误差之和不超过10分钟的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com