
分析 利用诱导公式以及二倍角的余弦函数,化简函数的解析式,然后求解函数的单调增区间.
解答 解:∵y=sin2($\frac{π}{12}$-x)+cos2($\frac{π}{12}$+x)
=$\frac{1-cos(\frac{π}{6}-2x)}{2}$+$\frac{1+cos(\frac{π}{6}+2x)}{2}$
=1+$\frac{1}{2}$×($\frac{\sqrt{3}}{2}$cos2x-$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x-$\frac{1}{2}$sin2x)
=1-$\frac{1}{2}$sin2x,
∴2kπ+$\frac{π}{2}$≤2x≤2kπ+$\frac{3π}{2}$,可解得函数的单调递增区间为:[kπ+$\frac{π}{4}$,kπ+$\frac{3π}{4}$],k∈Z.
点评 本题考查二倍角公式的应用,三角函数的单调性的应用,考查计算能力,属于基础题.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
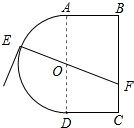 一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示,小球从A点出发以大小为5v的速度沿半圆O轨道滚到某点E处,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F,设∠AOE=θ弧度,小球从A到F所需时间为T.
一个玩具盘由一个直径为2米的半圆O和一个矩形ABCD构成,AB=1米,如图所示,小球从A点出发以大小为5v的速度沿半圆O轨道滚到某点E处,经弹射器以6v的速度沿与点E切线垂直的方向弹射到落袋区BC内,落点记为F,设∠AOE=θ弧度,小球从A到F所需时间为T.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成绩 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) | 合计 |
| 等级 | E | D | C | B | A | |
| 频数 | 2 | 24 | 36 | 30 | 8 | 100 |
| 频率 | 0.02 | 0.24 | 0.36 | 0.3 | 0.08 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z不可能是实数 | B. | z不可能是纯虚数 | C. | Rez•Imz≥0 | D. | Imz≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com