设点P是△ABC所在平面内一点，
，则点P是△ABC
| A．内心 | B．外心 | C．重心 | D．垂心 |
科目：高中数学 来源： 题型：填空题
（2009•聊城一模）由代数式的乘法法则类比推导向量的数量积的运算法则：
①“mn=nm”类比得到“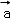
•
=•”；
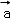②“（m+n）t=mt+nt”类比得到“（+）•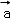
=•+•
”；
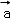③“t≠0，mt=nt⇒m=n”类比得到“≠0，
•=
•⇒=”；
④“|m•n|=|m|•|n|”类比得到“|•|=||•||”．
以上类比得到的正确结论的序号是 _________ （写出所有正确结论的序号）．
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
在等腰直角△ABC中，点O是斜边BC的中点，过点O的直线分别交直线AB、AC于不同的两点M、N，若
,则
的最大值为（ ）
A. 
B.1 C.2 D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
,则说明点P是三角形ACB的垂心，故选D.
是正方形ABCD的内接三角形,若
,则点C分线段BE所成的比为( ). 
，且关于
的函数
在
上有极值，则
与
的夹角范围（ ）
的夹角为
且
，在
中，
， 
，
为
中点，则
与圆
交于
两点，且
（其中
为坐标原点），则实数
的值为
则
的值为( )
，若
，则
．