
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 在
在![]() 上恰有两个不同的零点,求实数
上恰有两个不同的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)f(x)在(-∞,-1)递减;在(-1,+∞)递增;(2)![]() .
.
【解析】试题分析:(1)求出函数的导数,得到关于![]() 的方程,求出
的方程,求出![]() ,解关于导函数的不等式,求出函数的单调区间即可;
,解关于导函数的不等式,求出函数的单调区间即可;
(2)问题等价于![]() 在[-2,2]上恰有两个不同的实根.令g(x)=xex+x2+2x,求出函数的单调性求出g(x)的最小值,从而求出m的范围即可.
在[-2,2]上恰有两个不同的实根.令g(x)=xex+x2+2x,求出函数的单调性求出g(x)的最小值,从而求出m的范围即可.
试题解析:
(1)f'(x)=ex+xex+2ax+2,
∵f(x)在x=1处取得极值, ∴f'(-1)=0,解得a=1.经检验a=1适合,
∴f(x)=xex+x2+2x+1,f'(x)=(x+1)(ex+2),
当x∈(-∞,-1)时,f'(x)<0,∴f(x)在(-∞,-1)递减;
当x∈(-1+∞)时,f'(x)>0,∴f(x)在(-1,+∞)递增.
(2)函数y=f(x)-m-1在[-2,2]上恰有两个不同的零点,
等价于xex+x2+2x-m=0在[-2,2]上恰有两个不同的实根,
等价于xex+x2+2x=m在[-2,2]上恰有两个不同的实根.
令g(x)=xex+x2+2x,∴g'(x)=(x+1)(ex+2),
由(1)知g(x)在(-∞,-1)递减; 在(-1,+∞)递增.
g(x)在[-2,2]上的极小值也是最小值; ![]() . 又
. 又![]() ,g(2)=8+2e2>g(-2), ∴
,g(2)=8+2e2>g(-2), ∴![]() ,即
,即![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线![]() 与椭圆
与椭圆![]() 在第一象限内的交点是
在第一象限内的交点是![]() ,点
,点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 另一个焦点是
另一个焦点是![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的内切圆面积的最大值.
的内切圆面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)设![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,若存在点
,若存在点![]() ,满足
,满足![]() ,且线段
,且线段![]() 与
与![]() 互相平分(
互相平分(![]() 为原点),求
为原点),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 上一点
上一点![]() 到其焦点
到其焦点![]() 的距离为5.
的距离为5.
(1)求![]() 与
与![]() 的值;
的值;
(2)设动直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,问:在
两点,问:在![]() 轴上是否存在与
轴上是否存在与![]() 的取值无关的定点
的取值无关的定点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,用一平面去截球![]() ,所得截面面积为
,所得截面面积为![]() ,球心
,球心![]() 到截面的距离为3,
到截面的距离为3,![]() 为截面小圆圆心,
为截面小圆圆心,![]() 为截面小圆的直径.
为截面小圆的直径.
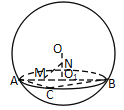
(1)计算球![]() 的表面积和体积;
的表面积和体积;
(2)若![]() 是截面小圆上一点,
是截面小圆上一点,![]() ,
,![]() 分别是线段
分别是线段![]() 和
和![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成的角(结果用反三角表示).
所成的角(结果用反三角表示).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某产品的销售额![]() 与广告费用
与广告费用![]() 之间的关系如下表:
之间的关系如下表:
| 0 | 1 | 2 | 3 | 4 |
| 10 | 15 |
| 30 | 35 |
若根据表中的数据用最小二乘法求得![]() 对
对![]() 的回归直线方程为
的回归直线方程为![]() ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.产品的销售额与广告费用成正相关
B.该回归直线过点![]()
C.当广告费用为10万元时,销售额一定为74万元
D.![]() 的值是20
的值是20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com