
【题目】设椭圆E: ![]() 的焦点在x轴上
的焦点在x轴上
(1)若椭圆E的焦距为1,求椭圆E的方程;
(2)设F1 , F2分别是椭圆E的左、右焦点,P为椭圆E上第一象限内的点,直线F2P交y轴于点Q,并且F1P⊥F1Q,证明:当a变化时,点P在某定直线上.
【答案】
(1)解:∵椭圆E的焦距为1,∴ ![]() ,解得
,解得 ![]() .
.
故椭圆E的方程为 ![]()
(2)解:设P(x0,y0),F1(﹣c,0),F2(c,0),其中 ![]() .
.
由题设可知:x0≠c.则直线F1P的斜率 ![]() =
= ![]() ,直线F2P的斜率
,直线F2P的斜率 ![]() =
= ![]() .
.
故直线F2P的方程为 ![]() .
.
令x=0,解得 ![]() .即点Q
.即点Q ![]() .
.
因此直线F1Q的斜率 ![]() =
= ![]() .
.
∵F1Q⊥F1P,∴ ![]() =
= ![]() .
.
化为 ![]() .
.
联立 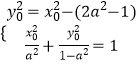 ,及x0>0,y0>0,
,及x0>0,y0>0,
解得 ![]() ,
, ![]() .
.
即点P在定直线x+y=1上
【解析】(1)利用椭圆的标准方程和几何性质即可得出 ![]() ,解出即可;(2)设P(x0 , y0),F1(﹣c,0),F2(c,0),其中
,解出即可;(2)设P(x0 , y0),F1(﹣c,0),F2(c,0),其中 ![]() .利用斜率的计算公式和点斜式即可得出直线F1P的斜率
.利用斜率的计算公式和点斜式即可得出直线F1P的斜率 ![]() =
= ![]() ,直线F2P的方程为
,直线F2P的方程为 ![]() .即可得出Q
.即可得出Q ![]() .得到直线F1Q的斜率
.得到直线F1Q的斜率 ![]() =
= ![]() .利用F1Q⊥F1P,可得
.利用F1Q⊥F1P,可得 ![]() =
= ![]() .化为
.化为 ![]() .与椭圆的方程联立即可解出点P的坐标.
.与椭圆的方程联立即可解出点P的坐标.
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
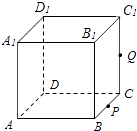
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S,则下列命题正确的是(写出所有正确命题的编号).
①当0<CQ< ![]() 时,S为四边形
时,S为四边形
②当CQ= ![]() 时,S为等腰梯形
时,S为等腰梯形
③当CQ= ![]() 时,S与C1D1的交点R满足C1R=
时,S与C1D1的交点R满足C1R= ![]()
④当 ![]() <CQ<1时,S为六边形
<CQ<1时,S为六边形
⑤当CQ=1时,S的面积为 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过P(4,-2),Q(-1,3)两点,且圆心C在直线x+y-1=0上.
(1)求圆C的方程;
(2)若直线l∥PQ,且l与圆C交于点A,B且以线段AB为直径的圆经过坐标原点,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有n位学生,每次活动均需该系k位学生参加(n和k都是固定的正整数),假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系k位学生,且所发信息都能收到,记该系收到李老师或张老师所发活动通知信息的学生人数为X.
(1)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(2)求使P(X=m)取得最大值的整数m.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设有直线![]() 和平面
和平面![]() ,则下列四个命题中,正确的是( )
,则下列四个命题中,正确的是( )
A. 若m∥α,n∥α,则m∥nB. 若mα,nα,m∥β,l∥β,则α∥β
C. 若α⊥β,mα,则m⊥βD. 若α⊥β,m⊥β,mα,则m∥α
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线的参数方程为 ![]() (t为参数),其中p>0,焦点为F,准线为l.过抛物线上一点M作l的垂线,垂足为E.若|EF|=|MF|,点M的横坐标是3,则p= .
(t为参数),其中p>0,焦点为F,准线为l.过抛物线上一点M作l的垂线,垂足为E.若|EF|=|MF|,点M的横坐标是3,则p= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com