
【题目】已知数列{an}的前n项和Sn=1+λan , 其中λ≠0.
(1)证明{an}是等比数列,并求其通项公式;
(2)若S5= ![]() ,求λ.
,求λ.
【答案】
(1)
解:∵Sn=1+λan,λ≠0.
∴an≠0.
当n≥2时,an=Sn﹣Sn﹣1=1+λan﹣1﹣λan﹣1=λan﹣λan﹣1,
即(λ﹣1)an=λan﹣1,
∵λ≠0,an≠0.∴λ﹣1≠0.即λ≠1,
即 ![]() =
= ![]() ,(n≥2),
,(n≥2),
∴{an}是等比数列,公比q= ![]() ,
,
当n=1时,S1=1+λa1=a1,
即a1= ![]() ,
,
∴an= ![]() (
( ![]() )n﹣1
)n﹣1
(2)
解:若S5= ![]() ,
,
则若S5=1+λ( ![]() (
( ![]() )4=
)4= ![]() ,
,
即( ![]() )5=
)5= ![]() ﹣1=﹣
﹣1=﹣ ![]() ,
,
则 ![]() =﹣
=﹣ ![]() ,得λ=﹣1
,得λ=﹣1
【解析】(1)根据数列通项公式与前n项和公式之间的关系进行递推,结合等比数列的定义进行证明求解即可.(2)根据条件建立方程关系进行求解就可.本题主要考查数列递推关系的应用,根据n≥2时,an=Sn﹣Sn﹣1的关系进行递推是解决本题的关键.考查学生的运算和推理能力.
【考点精析】本题主要考查了等比关系的确定和数列的通项公式的相关知识点,需要掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,对称轴为坐标轴,一条渐近线方程为![]() ,右焦点
,右焦点![]() ,双曲线的实轴为
,双曲线的实轴为![]() ,
,![]() 为双曲线上一点(不同于
为双曲线上一点(不同于![]() ,
,![]() ),直线
),直线![]() ,
,![]() 分别与直线
分别与直线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(![]() )求双曲线的方程.
)求双曲线的方程.
(![]() )证明
)证明![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市场调查发现,某种产品在投放市场的30天中,其销售价格P(元)和时间t(天)(t∈N)的关系如图所示 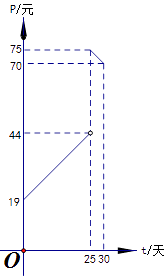
(1)写出销售价格P(元)和时间t(天)的函数解析式;
(2)若日销售量Q(件)与时间t(天)的函数关系是Q=﹣t+40(0≤t≤30,t∈N),求该商品的日销售金额y(元)与时间t(天)的函数解析式;
(3)问该产品投放市场第几天时,日销售金额最高?最高值为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于利用斜二侧法得到的直观图有下列结论:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形,以上结论正确的是( )
A. ①② B. ① C. ③④ D. ①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)某学校为了支持生物课程基地研究植物生长,计划利用学校空地建造一间室内面积为900m2的矩形温室,在温室内划出三块全等的矩形区域,分别种植三种植物,相邻矩形区域之间间隔1m,三块矩形区域的前、后与内墙各保留 1m 宽的通道,左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道,如图.设矩形温室的室内长为![]() (m),三块种植植物的矩形区域的总面积为
(m),三块种植植物的矩形区域的总面积为![]() (m2).
(m2).

(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为0的等差数列{an}的首项a1为a(a∈R).设数列的前n项和为Sn,且![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求数列{an}的通项公式及Sn;
(2)记![]() ,
,![]() .当n≥2时,求An与Bn.
.当n≥2时,求An与Bn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面内,定点A,B,C,D满足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,|
|,| ![]() ||
|| ![]() |=|
|=| ![]() ||
|| ![]() |=|
|=| ![]() ||
|| ![]() |=﹣4,动点P,M满足|
|=﹣4,动点P,M满足| ![]() |=2,
|=2, ![]() =
= ![]() ,则|
,则| ![]() |的最大值是 .
|的最大值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com