
【题目】如图,AB是圆柱![]() 的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,
的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,![]()
![]()
![]() :
:
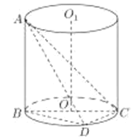
(1)求直线AC与平面ABD所成角的大小;
(2)求点B到平面ACD的距离;
(3)将四面体ABCD绕母线AB旋转一周,求由![]() 旋转而成的封闭几何体的体积;
旋转而成的封闭几何体的体积;
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
【解析】
(1)由AB⊥CD,BD⊥CD得出CD⊥平面ABD,故而∠CAD即为所求角,利用勾股定理得出AC,即可得出sin∠CAD;
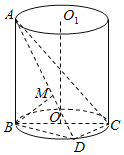
(2)过B作BM⊥AD,垂足为M,通过证明平面ABD⊥平面ACD得出BM⊥平面ACD,利用等面积法求出BM;
(3)△ACD绕AB旋转而成的封闭几何体为大圆锥中挖去一个小圆锥,使用作差法求出体积.
(1)∵AB⊥平面BCD,CD平面BCD,
∴AB⊥CD,
∵BC是圆O的直径,
∴BD⊥CD,
又BD平面ABD,AB平面ABD,AB∩BDE=B,
∴CD⊥平面ABD.
∴∠CAD是AC与平面ABD所成的角.
∵AB=BC=5,∴AC=5![]() ,
,
∴sin∠CAD![]() .
.
∴直线AC与平面ABD所成角的大小为![]() .
.
(2)过B作BM⊥AD,垂足为M,
由(1)得CD⊥平面ABD,CD平面ACD,
∴平面ABD⊥平面ACD,
又平面ABD∩平面ACD=AD,BM平面ABD,BM⊥AD,
∴BM⊥平面ACD.
∵BD![]() 4,∴AD
4,∴AD![]() .
.
∴BM![]() .即B到平面ACD的距离为
.即B到平面ACD的距离为![]() .
.
(3)线段AC绕AB旋转一周所得几何体为以BC为底面半径,以AB为高的圆锥,
线段AD绕AB旋转一周所得几何体为以BD为底面半径,以AB为高的圆锥,
∴△ACD绕AB旋转一周而成的封闭几何体的体积V![]() 15π.
15π.


科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣2x﹣4y+m=0.
(1)若圆C与直线l:x+2y﹣4=0相交于M、N两点,且|MN|![]() ,求m的值;
,求m的值;
(2)在(1)成立的条件下,过点P(2,1)引圆的切线,求切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据指令![]() (
(![]() ,
,![]() ),机器人在平面上能完成下列动作,先原地旋转弧度
),机器人在平面上能完成下列动作,先原地旋转弧度![]() (
(![]() 为正时,按逆时针方向旋转
为正时,按逆时针方向旋转![]() ,
,![]() 为负时,按顺时针方向旋转
为负时,按顺时针方向旋转![]() ),再朝其面对的方向沿直线行走距离r;
),再朝其面对的方向沿直线行走距离r;
(1)现机器人在平面直角坐标系的坐标原点,且面对x轴正方向,试给机器人下一个指令,使其移动到点![]() ;
;
(2)机器人在完成该指令后,发现在点![]() 处有一小球,正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令?(结果用反三角函数表示)
处有一小球,正向坐标原点作匀速直线滚动,已知小球滚动的速度为机器人直线行走速度的2倍,若忽略机器人原地旋转所需的时间,问机器人最快可在何处截住小球?并给出机器人截住小球所需的指令?(结果用反三角函数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】箱子里有16张扑克牌:红桃![]() 、
、![]() 、4,黑桃
、4,黑桃![]() 、8、7、4、3、2,草花
、8、7、4、3、2,草花![]() 、
、![]() 、6、5、4,方块
、6、5、4,方块![]() 、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
、5,老师从这16张牌中挑出一张牌来,并把这张牌的点数告诉了学生甲,把这张牌的花色告诉了学生乙,这时,老师问学生甲和学生乙:你们能从已知的点数或花色中推知这张牌是什么牌吗?于是,老师听到了如下的对话:学生甲:我不知道这张牌;学生乙:我知道你不知道这张牌;学生甲:现在我知道这张牌了;学生乙:我也知道了.则这张牌是( )
A. 草花5B. 红桃![]()
C. 红桃4D. 方块5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四面体A-BCD中,有两条棱的长为![]()
![]() ,其余棱的长度都为1;
,其余棱的长度都为1;
(1)若![]() ,且
,且![]() ,求二面角A-BC-D的余弦值;
,求二面角A-BC-D的余弦值;
(2)求a的取值范围,使得这样的四面体是存在的;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
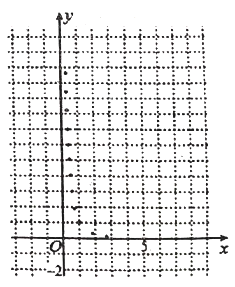
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为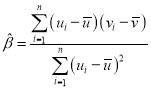 ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com