
【题目】已知数列![]() 是公差为正数的等差数列,其前
是公差为正数的等差数列,其前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)数列![]() 满足
满足![]() ,
,![]() .
.
①求数列![]() 的通项公式;
的通项公式;
②是否存在正整数![]() ,使得
,使得![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)an=2n-1(2)①bn=![]() ,n∈N*.②m=3,n=8
,n∈N*.②m=3,n=8
【解析】
试题分析:(1)先根据等差数列通项公式及求和公式得 ,解方程组得
,解方程组得![]() 或
或 (舍去),从而可得an=2n-1(2)①因为
(舍去),从而可得an=2n-1(2)①因为![]() =
=![]() ,所以利用叠加法可求数列
,所以利用叠加法可求数列![]() 的通项公式bn-b1=
的通项公式bn-b1=![]() ,即bn=
,即bn=![]() ,n∈N*.②由b2,bm,bn成等差数列,得b2+bn=2bm.解出
,n∈N*.②由b2,bm,bn成等差数列,得b2+bn=2bm.解出![]() 关系:2m=7-
关系:2m=7-![]() .最后根据分数整除性,得只有当n+1=9,即n=8时,m=3,满足题意
.最后根据分数整除性,得只有当n+1=9,即n=8时,m=3,满足题意
试题解析:(1)设数列{an}的公差为d,则d>0.
由a2·a3=15,S4=16,得
解得![]() 或
或 (舍去)
(舍去)
所以an=2n-1.
(2)①因为b1=a1,bn+1-bn=![]() ,
,
所以b1=a1=1,
bn+1-bn=![]() =
=![]() ,
,
即 b2-b1=![]() ,
,
b3-b2=![]() ,
,
……
bn-bn-1=![]() ,(n≥2)
,(n≥2)
累加得:bn-b1=![]() ,
,
所以bn=b1+![]() =1+
=1+![]() =
=![]() .
.
b1=1也符合上式.
故bn=![]() ,n∈N*.
,n∈N*.
②假设存在正整数m、n(m≠n),使得b2,bm,bn成等差数列,
则b2+bn=2bm.
又b2=![]() ,bn=
,bn=![]() =
=![]() -
-![]() ,bm=
,bm=![]() -
-![]() ,
,
所以![]() +(
+(![]() -
-![]() )=2(
)=2(![]() -
-![]() ),即
),即![]() =
=![]() +
+![]() ,
,
化简得:2m=![]() =7-
=7-![]() .
.
当n+1=3,即n=2时,m=2,(舍去);
当n+1=9,即n=8时,m=3,符合题意.
所以存在正整数m=3,n=8,使得b2,bm,bn成等差数列.


科目:高中数学 来源: 题型:
【题目】如图,公园有一块边长为2的等边三角形![]() 的地,现修成草坪,图中
的地,现修成草坪,图中![]() 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分, ![]() 在
在![]() 上,
上, ![]() 在
在![]() 上.
上.
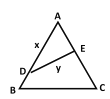
(1)设![]() ,
, ![]() ,请将
,请将![]() 表示为
表示为![]() 的函数,并求出该函数的定义域;
的函数,并求出该函数的定义域;
(2)如果![]() 是灌溉水管,为节约成本,希望它最短,
是灌溉水管,为节约成本,希望它最短, ![]() 的位置应在哪里?如果
的位置应在哪里?如果![]() 是参观线路,则希望它最长,
是参观线路,则希望它最长, ![]() 的位置又应在哪里?请予以说明.
的位置又应在哪里?请予以说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某初级中学有三个年级,各年级男、女生人数如下表:
初一年级 | 初二年级 | 初三年级 | |
女生 | 370 | z | 200 |
男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求z的值;
(2)用分层抽样的方法在初三年级中抽取一个容量为5的样本,将该样本看成一个总体,从中任选2名学生,求至少有1名女生的概率;
(3)用随机抽样的方法从初二年级女生中选出8人,测量它们的左眼视力,结果如下:1.2, 1.5, 1.2, 1.5, 1.5, 1.3, 1.0, 1.2.把这8人的左眼视力看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测验中,有6位同学的平均成绩为75分, 用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学的成绩如下:
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知棱长为l的正方体![]() 中,E,F,M分别是AB、AD、
中,E,F,M分别是AB、AD、![]() 的中点,又P、Q分别在线段
的中点,又P、Q分别在线段![]() 上,且
上,且![]() ,设面
,设面![]() 面MPQ=
面MPQ=![]() ,则下列结论中不成立的是( )
,则下列结论中不成立的是( )

A.![]() 面ABCD
面ABCD
B.![]() AC
AC
C.面MEF与面MPQ不垂直
D.当x变化时,![]() 不是定直线
不是定直线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com