Question

9．如图．已知ABCD-A₁B₁C₁D₁是棱长为3的正方体，点E在AA₁上，点F在CC₁上，G在BB₁上，且AE=FC₁=B₁G=1．H是B₁C₁的中点．
（1）求证：E，B，F，D₁四点共面：
（2）求证：平面A₁GH∥平面BED₁F．

Answer 1

分析 （1）在DD₁上取点N，使DN=1，连接EN，CN，易得四边形ADNE是平行四边形，以及四边形BCNE是平行四边形，由此推知CN∥BE，则FD₁∥BE，得到E、B、F、D₁四点共面；
（2）利用三角形相似证明HG∥FB，由（1）知，A₁G∥BE，从而可证平面A₁GH∥平面BED₁F．

解答 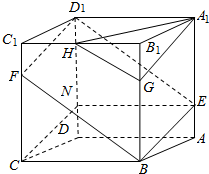证明：（1）如图：

在DD₁上取一点N使得DN=1，
连接CN，EN，则AE=DN=1．CF=ND₁=2、
因为CF∥ND₁所以四边形CFD₁N是平行四边形，
所以D₁F∥CN．
同理四边形DNEA是平行四边形，所以EN∥AD，且EN=AD，
又BC∥AD，且AD=BC，所以EN∥BC，EN=BC，
所以四边形CNEB是平行四边形，
所以CN∥BE，
所以D₁F∥BE，
所以E，B，F，D₁四点共面；
（2）因为H是B₁C₁的中点，所以B₁H=$\frac{3}{2}$，
因为B₁G=1，所以 $\frac{{B}_{1}G}{{B}_{1}H}$=$\frac{2}{3}$，
因为 $\frac{FC}{BC}$=$\frac{2}{3}$，且∠FCB=∠GB₁H=90°，
所以△B₁HG∽△CBF，
所以∠B₁GH=∠CFB=∠FBG，
所以HG∥FB，
由（1）知，A₁G∥BE且HG∩A₁G=G，FB∩BE=B，
所以平面A₁GH∥平面BED₁F．

点评 本题主要考查了了共面的判定，考查面面平行的判定，考查对基础知识的综合应用能力和基本定理的掌握能力，属于中档题．