【题目】在△ABC中，（5a﹣4c）cosB﹣4bcosC=0．
（1）求cosB的值；
（2）若c=5，b= 
，求△ABC的面积S．
【答案】
（1）解：∵（5a﹣4c）cosB﹣4bcosC=0．
∴5sinAcosB=4sinCcosB+4sinBcosC=4sin（B+C）=4sinA，
∴cosB= 
．
（2）解：由余弦定理得cosB= 
= ，即 
= ，解得a=3或a=5．
∵cosB= ，∴sinB= 
．
∴当a=3时，S△ABC= 
acsinB= 
= 
，
当a=5时，S△ABC= acsinB= 
= 
．
【解析】（1）利用正弦定理边化角，使用和角公式化简即可得出cosB；（2）利用余弦定理计算a，在代入面积公式S= 
即可求出面积．
【考点精析】根据题目的已知条件，利用正弦定理的定义和余弦定理的定义的相关知识可以得到问题的答案，需要掌握正弦定理:
；余弦定理:
;
;
．
导学全程练创优训练系列答案科目：高中数学 来源： 题型：
【题目】已知向量 
=（1，2）， 
=（x，1）；
（1）若（ +2 ）⊥（2 ﹣ ）时，求x的值；
（2）若向量 与向量 的夹角为锐角，求x的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知以点C（t， 
）（t∈R，t≠0）为圆心的圆过原点O．
（1）设直线3x+y﹣4=0与圆C交于点M、N，若|OM|=|ON|，求圆C的方程；
（2）在（1）的条件下，设B（0，2），且P、Q分别是直线l：x+y+2=0和圆C上的动点，求|PQ|﹣|PB|的最大值及此时点P的坐标．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【南京市、盐城市2017届高三年级第二次模拟】（本小题满分14分）
在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD，然后在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒（如图）．设小正方形边长为x厘米，矩形纸板的两边AB，BC的长分别为a厘米和b厘米，其中a≥b．
（1）当a＝90时，求纸盒侧面积的最大值；
（2）试确定a，b，x的值，使得纸盒的体积最大，并求出最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
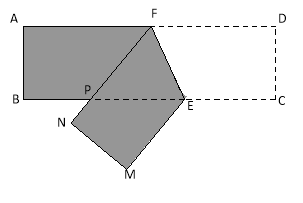
【题目】【2017南通一模】（本题满分16分）如图，某机械厂要将长6m，宽2m的长方形铁皮ABCD进行裁剪。已知点F为AD的中点，点E在边BC上，裁剪时先将四边形CDFE沿直线EF翻折到MNFE处（点C，D分别落在直线BC下方点M，N处，FN交边BC于点P），再沿直线PE裁剪。
（1）当
时，试判断四边形MNPE的形状，并求其面积；
（2）若使裁剪得到的四边形MNPE面积最大，请给出裁剪方案，并说明理由。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下图是容量为100的样本的频率分布直方图，则样本数据在[6,10)内的频率和频数分别是（ ）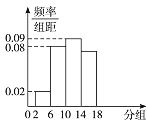
A.0.32,32
B.0.08,8
C.0.24,24
D.0.36,36
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】【2017辽宁鞍山市最后一次模】如图所示,在三棱锥
中,侧面
, 
是全等的直角三角形, 
是公共的斜边且
, 
,另一侧面
是正三角形.
（1）求证： 
；
（2）若在线段
上存在一点
,使
与平面
成
角,试求二面角
的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4―4：坐标系与参数方程]
在直角坐标系xOy中，曲线C的参数方程为
（θ为参数），直线l的参数方程为
.
（1）若a=1，求C与l的交点坐标；
（2）若C上的点到l的距离的最大值为
，求a.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
