.(本小题满分14分)
已知单调递增的等比数列
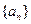
满足:
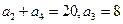
;
(1)求数列
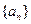
的通项公式;
(2)若
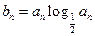
,数列
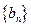
的前n项和为
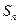
,求
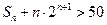
成立的正整数 n的最小值.
【解】(1)设等比数列
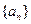
的首项为
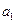
,公比为q,
依题意,有
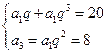
,解之得
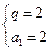
或

; (…………4分)
又
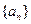
单调递增,∴
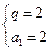
,∴
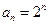
. (…………6分)
(2)依题意,
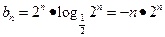
,


(…………8分)
∴
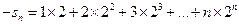
①,
∴
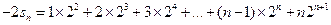
②,
∴①-②得
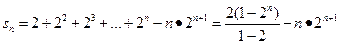
=
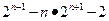
;

(……12分)
∴
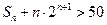
即为
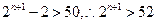
,
∵当n≤4时,
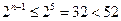
;当n≥5时,
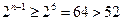
.
∴使
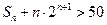
成立的正整数n的最小值为5. (…………14分)
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
.(本小题满分14分)
已知数列
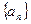
满足
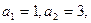
且
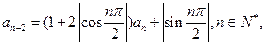
(1)求
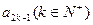
;
(2)数列
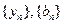
满足
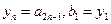
,且
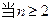
时
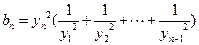
.
证明当
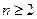
时,
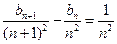
;
(3)在(2)的条件下,试比较
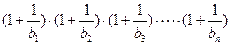
与4的大小关系.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知直角三角形
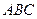
的三边
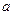
、
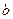
、
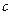
成等差且均为整数,公差为
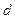
,则下列命题不正确的是( )
A.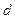 为整数. 为整数. | B.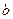 为 为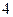 的倍数 的倍数 | C.外接圆的半径为整数 | D.内切圆半径为整数 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知数列
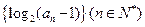
为等差数列,且
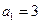
,
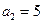
,则
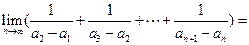
___

_________.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在等差数列
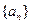
中,有
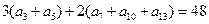
,则此数列的前13项之和为( )
A 24 B 39 C 52 D 104
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分14分)
在数列
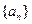
中,
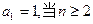
时,其前
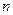
项和
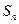
满足:
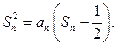
(Ⅰ)求
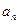
;
(Ⅱ)令
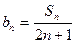
,求数列
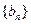
的前项和
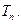
查看答案和解析>>

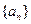 满足:
满足: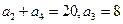 ;
;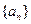 的通项公式;
的通项公式;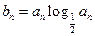 ,数列
,数列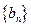 的前n项和为
的前n项和为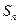 ,求
,求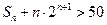 成立的正整数 n的最小值.
成立的正整数 n的最小值. 阅读快车系列答案
阅读快车系列答案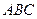 的三边
的三边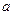 、
、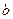 、
、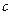 成等差且均为整数,公差为
成等差且均为整数,公差为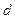 ,则下列命题不正确的是( )
,则下列命题不正确的是( )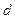 为整数.
为整数.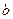 为
为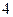 的倍数
的倍数