
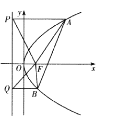
【题目】设椭圆C:![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,上顶点为A,在x轴负半轴上有一点B,满足
,上顶点为A,在x轴负半轴上有一点B,满足![]() 为线段
为线段![]() 的中点,且AB⊥
的中点,且AB⊥![]() 。
。
(I)求椭圆C的离心率;
(II)若过A、B、![]() 三点的圆与直线
三点的圆与直线![]() :
:![]() 相切,求椭圆C的方程;
相切,求椭圆C的方程;
(III)在(I)的条件下,过右焦点![]() 作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
作斜率为k的直线与椭圆C交于M,N两点,在x轴上是否存在点P(m,0)使得以PM,PN为邻边的平行四边形是菱形?如果存在,求出m的取值范围;如果不存在,说明理由。
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() 。
。
【解析】分析:(Ⅰ)由题意可得在在直角三角形![]() 中有
中有![]() ,即
,即![]() ,整理可得
,整理可得![]() .(Ⅱ)由题意可得过A、B、F2三点的圆的圆心为F1(-c,0),半径r=
.(Ⅱ)由题意可得过A、B、F2三点的圆的圆心为F1(-c,0),半径r=![]()
=2c,根据直线![]() 与圆相切可得
与圆相切可得![]() ,解得c=1,从而
,解得c=1,从而![]() ,
,![]() ,可得椭圆的方程.(Ⅲ)由条件可设直线MN的方程为
,可得椭圆的方程.(Ⅲ)由条件可设直线MN的方程为![]() ,与椭圆方程联立消元后得到一元二次方程,结合根据系数的关系可得MN的中点Q的坐标为
,与椭圆方程联立消元后得到一元二次方程,结合根据系数的关系可得MN的中点Q的坐标为![]() ,若以PM,PN为邻边的平行四边形是菱形,则
,若以PM,PN为邻边的平行四边形是菱形,则![]() ,由此得到
,由此得到![]() ,整理得
,整理得 ,最后可求得
,最后可求得![]() .
.
详解:(I)∵AB⊥AF2,![]() 为
为![]() 的中点,
的中点,
∴![]()
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
即椭圆C的离心率为![]() .
.
(II)过A、B、F2三点的圆的圆心为F1(-c,0),半径r=![]() =2c.
=2c.
∵直线![]() :
:![]() 相切,
相切,
∴![]() ,
,
解得c=1.
又![]() ,
,
∴![]() ,
,
∴![]() .
.
∴椭圆C的方程为![]() .
.
(III)由(I)知,F2(1,0),直线MN的方程为![]() ,
,
由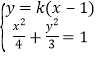 消去y整理得
消去y整理得![]()
∵直线与椭圆C交于M,N两点,
∴![]() .
.
设M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),
),
则![]()
∴![]() ,
,
∴MN的中点Q的坐标为![]() ,
,
若以PM,PN为邻边的平行四边形是菱形,
则![]() ,
,
∴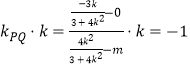
整理得 ,
,
∵![]() ,
,
![]() ,
,
∴![]() .
.
∴![]() .
.
故存在满足题意的点P,且m的取值范围是(![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】一个盒子中装有标号为1,2,3,4,5的5张标签,随机地依次选取两张标签,根据下列条件求两张标签上的数字为相等整数的概率;
(1)标签的选取是不放回的;
(2)标签的选取是有放回的.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某种型号的电视机零配件,为了预测今年![]() 月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度
月份该型号电视机零配件的市场需求量,以合理安排生产,工厂对本年度![]() 月份至
月份至![]() 月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价
月份该型号电视机零配件的销售量及销售单价进行了调查,销售单价![]() (单位:元)和销售量
(单位:元)和销售量![]() (单位:千件)之间的
(单位:千件)之间的![]() 组数据如下表所示:
组数据如下表所示:
月份 |
|
|
|
|
|
|
销售单价 |
|
|
|
|
|
|
销售量 |
|
|
|
|
|
|
(1)根据1至![]() 月份的数据,求
月份的数据,求![]() 关于
关于![]() 的线性回归方程(系数精确到
的线性回归方程(系数精确到![]() );
);
(2)结合(1)中的线性回归方程,假设该型号电视机零配件的生产成本为每件![]() 元,那么工厂如何制定
元,那么工厂如何制定![]() 月份的销售单价,才能使该月利润达到最大(计算结果精确到
月份的销售单价,才能使该月利润达到最大(计算结果精确到![]() )?
)?
参考公式:回归直线方程![]() ,其中
,其中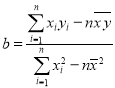 .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上
上![]() 两点,在抛物线的准线上的射影分别为
两点,在抛物线的准线上的射影分别为![]() .
.
(1)如图,若![]() 点在线段
点在线段![]() 上,过
上,过![]() 作
作![]() 的平行线
的平行线![]() 与抛物线准线交于
与抛物线准线交于![]() ,证明:
,证明:![]() 是
是![]() 的中点;
的中点;
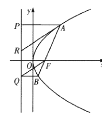
(2)如图,若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌计算机售后保修期为1年,根据大量的维修记录资料,这种品牌的计算机在使用一年内需要维修1次的占15%,需要维修2次的占6%,需要维修3次的占4%.
(1)某人购买了一台这个品牌的计算机,设![]() =“一年内需要维修k次”,k=0,1,2,3,请填写下表:
=“一年内需要维修k次”,k=0,1,2,3,请填写下表:
事件 |
|
|
|
|
概率 |
事件![]() 是否满足两两互斥?是否满足等可能性?
是否满足两两互斥?是否满足等可能性?
(2)求下列事件的概率:
①A=“在1年内需要维修”;
②B=“在1年内不需要维修”;
③C=“在1年内维修不超过1次”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线C:x2=2py (p>0) 的焦点,点A(m,3)在抛物线C上,且|AF|=5,若点P是抛物线C上的一个动点,设点P到直线![]() 的距离为
的距离为![]() ,设点P到直线
,设点P到直线![]() 的距离为
的距离为![]() .
.
(1)求抛物线C的方程;
(2) 求![]() 的最小值;
的最小值;
(3)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中尝试进行课堂改革.现高一有![]() 两个成绩相当的班级,其中
两个成绩相当的班级,其中![]() 班级参与改革,
班级参与改革,![]() 班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过
班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过![]() 分的为进步明显,得到如下列联表.
分的为进步明显,得到如下列联表.
进步明显 | 进步不明显 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)是否有![]() 的把握认为成绩进步是否明显与课堂是否改革有关?
的把握认为成绩进步是否明显与课堂是否改革有关?
(2)按照分层抽样的方式从![]() 班中进步明显的学生中抽取
班中进步明显的学生中抽取![]() 人做进一步调查,然后从
人做进一步调查,然后从![]() 人中抽
人中抽![]() 人进行座谈,求这
人进行座谈,求这![]() 人来自不同班级的概率.
人来自不同班级的概率.
附: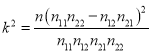 ,当
,当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关.
有关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少儿游泳队需对队员进行限时的仰卧起坐达标测试.已知队员的测试分数![]() 与仰卧起坐
与仰卧起坐
个数![]() 之间的关系如下:
之间的关系如下: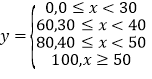 ;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
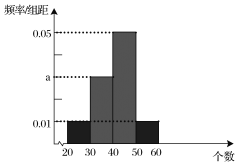
(1)计算![]() 值;
值;
(2)以此样本的频率作为概率,求
①在本次达标测试中,“喵儿”得分等于![]() 的概率;
的概率;
②“喵儿”在本次达标测试中可能得分的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com