
【题目】如图,在△ABC中,AB=2,3acosB﹣bcosC=ccosB,点D在线段BC上. 
(1)若∠ADC= ![]() ,求AD的长;
,求AD的长;
(2)若BD=2DC,△ACD的面积为 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)解:∵3acosB﹣bcosC=ccosB,
∴3sinAcosB=sinCcosB+sinBcosC,3sinAcosB=sin(B+C),
∵B+C=π﹣A,
∴3sinAcosB=sinA,
∵A∈(0,π),
∴sinA>0, ![]() .
.
∵B∈(0,π),
∴ ![]() .
.
∵ ![]() ,
,
∴ ![]() ,
,
在△ABD中,由正弦定理得, ![]() ,
,
∴ ![]() ,
, ![]() .
.
(2)解:设DC=a,则BD=2a,
∵BD=2DC,△ACD的面积为 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴a=2.…(8分)
∴ ![]() ,由正弦定理可得
,由正弦定理可得 ![]() ,
,
∴ ![]() .
. ![]() ,
,
∴ ![]() ,
,
∵sin∠ADB=sin∠ADC,
∴ ![]() .
.
【解析】(1)由三角形内角和定理,两角和的正弦函数公式,正弦定理化简已知等式可得3sinAcosB=sinA,结合sinA>0,可求 ![]() ,利用同角三角函数基本关系式可求sinB,进而可求
,利用同角三角函数基本关系式可求sinB,进而可求 ![]() ,由正弦定理即可求得AD的值.(2)设DC=a,则BD=2a,利用已知及三角形面积公式可求a,利用余弦定理可求AC,由正弦定理可得
,由正弦定理即可求得AD的值.(2)设DC=a,则BD=2a,利用已知及三角形面积公式可求a,利用余弦定理可求AC,由正弦定理可得 ![]() ,结合sin∠ADB=sin∠ADC,即可求值得解.
,结合sin∠ADB=sin∠ADC,即可求值得解.
【考点精析】掌握正弦定理的定义是解答本题的根本,需要知道正弦定理:![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,某自行车手从O点出发,沿折线O﹣A﹣B﹣O匀速骑行,其中点A位于点O南偏东45°且与点O相距20 ![]() 千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°﹣α)(其中sinα=
千米.该车手于上午8点整到达点A,8点20分骑至点C,其中点C位于点O南偏东(45°﹣α)(其中sinα= ![]() ,0°<α<90°)且与点O相距5
,0°<α<90°)且与点O相距5 ![]() 千米(假设所有路面及观测点都在同一水平面上).
千米(假设所有路面及观测点都在同一水平面上).
(1)求该自行车手的骑行速度;
(2)若点O正西方向27.5千米处有个气象观测站E,假定以点E为中心的3.5千米范围内有长时间的持续强降雨.试问:该自行车手会不会进入降雨区,并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数f(x)与g(x)和区间D,如果存在x0∈D,使|f(x0)﹣g(x0)|≤1,则称x0是函数f(x)与g(x)在区间D上的“友好点”.现给出两个函数:
①f(x)=x2 , g(x)=2x﹣2;② ![]() ,g(x)=x+2;
,g(x)=x+2;
③f(x)=e﹣x , ![]() ;④f(x)=lnx,g(x)=x.
;④f(x)=lnx,g(x)=x.
则在区间(0,+∞)上存在唯一“友好点”的是 . (填上所有正确的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂拟生产甲、乙两种适销产品,每件销售收入分别为3000元,2000元.甲、乙产品都需要在A、B两种设备上加工,在每台A、B设备上加工一件甲所需工时分别为1![]() ,2
,2![]() ,加工一件乙设备所需工时分别为2
,加工一件乙设备所需工时分别为2![]() ,1
,1![]() .A、B两种设备每月有效使用台时数分别为400
.A、B两种设备每月有效使用台时数分别为400![]() 和500
和500![]() ,分别用
,分别用![]() 表示计划每月生产甲,乙产品的件数.
表示计划每月生产甲,乙产品的件数.
(Ⅰ)用![]() 列出满足生产条件的数学关系式,并画出相应的平面区域;
列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问分别生产甲、乙两种产品各多少件,可使收入最大?并求出最大收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),圆C的参数方程为
为参数),圆C的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,
为参数),以坐标原点O为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求直线l和圆C的极坐标方程;
(Ⅱ)设直线l和圆C相交于A,B两点,求弦AB与其所对劣弧所围成的图形面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机给人们的生活带来便利的同时,也给青少年的成长带来不利的影响,有人沉迷于手机游戏无法自拔,严重影响了自己的学业,某学校随机抽取![]() 个班,调查各班带手机来学校的人数,所得数据的茎叶图如图所示.以组距为
个班,调查各班带手机来学校的人数,所得数据的茎叶图如图所示.以组距为![]() 将数据分组成
将数据分组成![]() ,
,![]() ,…,
,…,![]() ,
,![]() 时,所作的频率分布直方图是( )
时,所作的频率分布直方图是( )

A.  B.
B. 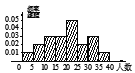
C. 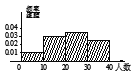 D.
D. 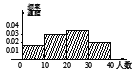
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com