
 在某次试验中,有两个试验数据x,y,统计的结果如下面的表格
在某次试验中,有两个试验数据x,y,统计的结果如下面的表格| x | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 3 | 4 | 4 | 5 |
| ∧ |
| b |
| |||||||
|
| ∧ |
| a |
. |
| y |
| ∧ |
| b |
. |
| x |
| ∧ |
| y |
| ∧ |
| b |
| ∧ |
| a |
| 序号 | x | y | x2 | xy |
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| ∑ |
. |
| x |
. |
| y |
| 5 |
 |
| i=1 |
| 5 |
 |
| i=1 |
| ? |
| b |
| ? |
| a |
| 序号 | x | y | x2 | xy |
| 1 | 1 | 2 | 1 | 2 |
| 2 | 2 | 3 | 4 | 6 |
| 3 | 3 | 4 | 9 | 12 |
| 4 | 4 | 4 | 16 | 16 |
| 5 | 5 | 5 | 25 | 25 |
| ∑ | 15 | 18 | 55 | 61 |
. |
| x |
. |
| y |
| ? |
| b |
| ? |
| a |
| ? |
| y |
| ? |
| y |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
 在某次试验中,有两个试验数据x,y统计的结果如下面的表格:
在某次试验中,有两个试验数据x,y统计的结果如下面的表格:| x | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 3 | 4 | 4 | 5 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 9 |
| lim |
| n→∞ |
| x2 |
| 9 |
| y2 |
| 4 |
| 1 |
| x |
| 1 |
| a |
查看答案和解析>>
科目:高中数学 来源:2013届河南省高二下学期第一次月考文科数学试卷 题型:解答题
在某次试验中,有两个试验数据x,y,统计的结果如下面的表格1.
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
2 |
3 |
4 |
4 |
5 |
|


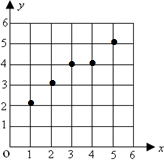
(1)在给出的坐标系中画出x,y的散点图。
(2)补全表格2,然后根据表格2的内容和公式 ,
,

1求出y对x的回归直线方程 中回归系数
中回归系数
2估计当x为10时 的值是多少?
的值是多少?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省湛江市高二(下)期末数学试卷(理科)(解析版) 题型:解答题
| x | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 3 | 4 | 4 | 5 |
 ;
;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com