
【题目】某颜料公司生产A,B两种产品,其中生产每吨A产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨B产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一天之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果A产品的利润为300元/吨,B产品的利润为200元/吨,设公司计划一天内安排生产A产品x吨,B产品y吨.
(I)用x,y列出满足条件的数学关系式,并在下面的坐标系中画出相应的平面区域;
(II)该公司每天需生产A,B产品各多少吨可获得最大利润,最大利润是多少?

【答案】(Ⅰ)见解析(Ⅱ)该公司每天需生产甲产品40吨,乙产品10吨可获得最大利润,最大利润为14000元.
【解析】分析:(Ⅰ)由题意得到变量x,y满足的条件即可得到所求,然后在坐标系内画出图形即可.(Ⅱ)由题意的利润z=300x+200y,然后据线性规划的有关知识解题可得所求.
详解:(I)设该公司一天安排生产甲产品x吨,乙产品y吨,则x,y满足条件的数学关系式为 .
.
画出该二元一次不等式组表示的平面区域(可行域)如下图所示.

(II)设利润为z元,由题意得z=300x+200y,
可得![]() ,
,
平移直线![]() ,结合图形可得当直线
,结合图形可得当直线![]() 经过可行域上的点A时,截距
经过可行域上的点A时,截距![]() 最大,此时z页最大.
最大,此时z页最大.
解方程组![]() 得
得![]() ,即
,即![]() .
.
∴![]() =300x+200y=14000.
=300x+200y=14000.
答:该公司每天需生产甲产品40吨,乙产品10吨时可获得最大利润,且最大利润为14000元.


科目:高中数学 来源: 题型:
【题目】经销商小王对其所经营的某一型号二手汽车的使用年数![]() (0<
(0<![]() ≤10)与销售价格
≤10)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅰ)试求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(附:回归方程![]() 中,
中,
(Ⅱ)已知每辆该型号汽车的收购价格为![]() 万元,根据(Ⅰ)中所求的回归方程,
万元,根据(Ⅰ)中所求的回归方程,
预测![]() 为何值时,小王销售一辆该型号汽车所获得的利润
为何值时,小王销售一辆该型号汽车所获得的利润![]() 最大.
最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且满足
上,且满足![]() ,(
,(![]() 为坐标原点).
为坐标原点).
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 作斜率乘积为1的两条不重合的直线
作斜率乘积为1的两条不重合的直线![]() ,且
,且![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标.
过定点,并求出定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.
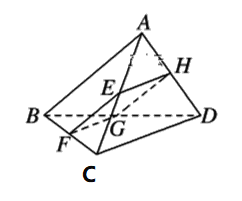
(1)求证:AB∥平面EFGH
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com