
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ![]() ,过点
,过点 ![]() 的直线
的直线 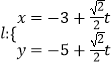 (
( ![]() 为参数)与曲线
为参数)与曲线 ![]() 相交于点
相交于点 ![]() ,
, ![]() 两点.
两点.
(1)求曲线 ![]() 的平面直角坐标系方程和直线
的平面直角坐标系方程和直线 ![]() 的普通方程;
的普通方程;
(2)求 ![]() 的值.
的值.
 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)上的函数f(x)满足f′(x)+2f(x)= ![]() ,且f(1)=
,且f(1)= ![]() ,则不等式f(lnx)>f(3)的解集为( )
,则不等式f(lnx)>f(3)的解集为( )
A.(﹣∞,e3)
B.(0,e3)
C.(1,e3)
D.(e3 , +∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
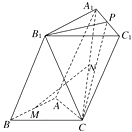
【题目】如图,已知三棱柱 ![]() ,侧面
,侧面 ![]() .
.
(Ⅰ)若 ![]() 分别是
分别是 ![]() 的中点,求证:
的中点,求证: ![]() ;
;
(Ⅱ)若三棱柱 ![]() 的各棱长均为2,侧棱
的各棱长均为2,侧棱 ![]() 与底面
与底面 ![]() 所成的角为
所成的角为 ![]() ,问在线段
,问在线段 ![]() 上是否存在一点
上是否存在一点 ![]() ,使得平面
,使得平面 ![]() ?若存在,求
?若存在,求 ![]() 与
与 ![]() 的比值,若不存在,说明理由.
的比值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区工会利用“健步行![]() ” 开展健步走积分奖励活动.会员每天走5 千步可获积分30分(不足5千步不积分), 每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了 1000名会员,统计了当天他们的步数,并将样本数据分为
” 开展健步走积分奖励活动.会员每天走5 千步可获积分30分(不足5千步不积分), 每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了 1000名会员,统计了当天他们的步数,并将样本数据分为![]() ,
,![]() 九组,整理得到如图频率分布直方图:
九组,整理得到如图频率分布直方图:
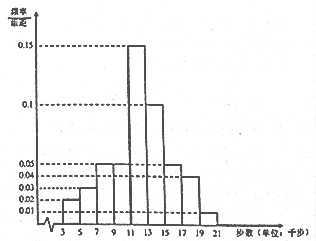
(1)求当天这1000名会员中步数少于11千步的人数;
(2)从当天步数在![]() 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
(3)写出该组数据的中位数(只写结果).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为521,则由此可估计π的近似值为( ) 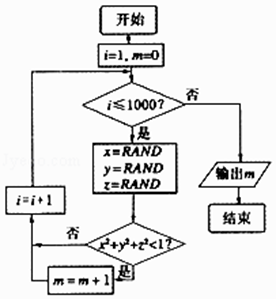
A.3.119
B.3.126
C.3.132
D.3.151
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,偏差是指个别测定值与测定的平均值之差,在成绩统计中,我们把某个同学的某科考试成绩与该科班平均分的差叫某科偏差,班主任为了了解个别学生的偏科情况,对学生数学偏差x(单位:分)与物理偏差y(单位:分)之间的关系进行学科偏差分析,决定从全班56位同学中随机抽取一个容量为8的样本进行分析,得到他们的两科成绩偏差数据如下:
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
数学偏差x | 20 | 15 | 13 | 3 | 2 | -5 | -10 | -18 |
物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | -0.5 | -2.5 | -3.5 |
(1)已知x与y之间具有线性相关关系,求y关于x的线性回归方程;
(2)若这次考试该班数学平均分为118分,物理平均分为90.5,试预测数学成绩126分的同学的物理成绩.
参考公式:  ,.
,.![]()
参考数据: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com