
【题目】如图,等边三角形![]() 的中线
的中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,下列命题中,正确的是( )
旋转过程中的一个图形,下列命题中,正确的是( )

A.动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上
上
B.恒有平面![]() 平面
平面![]()
C.三棱锥![]() 的体积有最大值
的体积有最大值
D.旋转过程中二面角![]() 的平面角始终为
的平面角始终为![]()
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABED中,AB//DE,AB![]() BE,点C在AB上,且AB
BE,点C在AB上,且AB![]() CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE
CD,AC=BC=CD=2,现将△ACD沿CD折起,使点A到达点P的位置,且PE![]() .
.
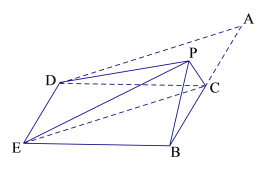
(1)求证:平面PBC ![]() 平面DEBC;
平面DEBC;
(2)求三棱锥P-EBC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在梯形ABCD中,AB//CD,AB=3,CD=6,过A,B分别作CD的垂线,垂足分别为E,F,已知DE=1,AE=3,将梯形ABCD沿AE,BF同侧折起,使得平面ADE⊥平面ABFE,平面ADE∥平面BCF,得到图2.
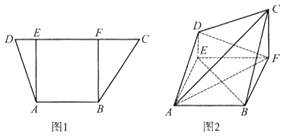
(1)证明:BE//平面ACD;
(2)求三棱锥C﹣AED的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自2016年1月1日全面实施二孩政策以来,为了了解生二孩意愿与年龄段是否有关,某市选取“75后”和“80后”两个年龄段的已婚妇女作为调查对象,进行了问卷调查,共调查了40名“80后”,40名“75后”,其中调查的“80后”有10名不愿意生二孩,其余的全部愿意生二孩;调查的“75后”有5人不愿意生二孩,其余的全部愿意生二孩.
(1)根据以上数据完成下列![]() 列联表;
列联表;
年龄段 | 不愿意 | 愿意 | 合计 |
“80后” | |||
“75后” | |||
合计 |
(2)根据![]() 列联表,能否在犯错误的概率不超过0.05的前提下,认为“生二孩意愿与年龄段有关”?请说明理由.
列联表,能否在犯错误的概率不超过0.05的前提下,认为“生二孩意愿与年龄段有关”?请说明理由.
参考公式: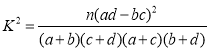 (其中
(其中![]() )
)
附表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com