
【题目】某地上年度电价为0.8元,年用电量为1亿千瓦时.本年度计划将电价调至0.55元~0.75元之间,经测算,若电价调至x元,则本年度新增用电量y(亿千瓦时)与(x﹣0.4)元成反比例.又当x=0.65时,y=0.8.
(1)求y与x之间的函数关系式;
(2)若每千瓦时电的成本价为0.3元,则电价调至多少时,本年度电力部门的收益将比上年增加20%?[收益=用电量×(实际电价﹣成本价)].
【答案】
(1)解:∵y与(x﹣0.4)成反比例,∴设 ![]() .
.
把x=0.65,y=0.8代入上式,得k=0.2,∴ ![]() ,
,
即y与x之间的函数关系式为 ![]()
(2)解:根据题意,得( ![]() )(x﹣0.3)=1×(0.8﹣0.3)×(1+20%).
)(x﹣0.3)=1×(0.8﹣0.3)×(1+20%).
整理,得x2﹣1.1x+0.3=0,解得x1=0.5,x2=0.6.
经检验x1=0.5,x2=0.6都是所列方程的根.
∵x的取值范围是0.55~0.75,故x=0.5不符合题意,应舍去.∴x=0.6
答:当电价调至0.6元时,本年度电力部门的收益将比上年度增加20%.
【解析】(1)设出函数解析式,代入x=0.65时,y=0.8,即可求得函数解析式;(2)利用收益=用电量×(实际电价﹣成本价),建立方程,即可求得结论.


科目:高中数学 来源: 题型:
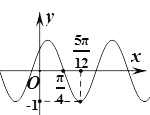
【题目】函数![]() (其中
(其中![]() )的部分图象如图所示,为了得到
)的部分图象如图所示,为了得到![]() 的图象,只要将
的图象,只要将![]() 的图象
的图象
A. 先向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
B. 先向右平移![]() 个单位长度,再把所得各点的横坐标伸长到原来的
个单位长度,再把所得各点的横坐标伸长到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
C. 先向左平移![]() 个单位长度 ,再把所得各点的横坐标缩短到原来的
个单位长度 ,再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
D. 先向左平移![]() 个单位长度, 再把所得各点的横坐标缩短到原来的
个单位长度, 再把所得各点的横坐标缩短到原来的![]() 倍,纵坐标不变
倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了对某课题进行讨论研究,用分层抽样的方法从三所高校A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校 | 相关人数 | 抽取人数 |
A | x | 1 |
B | 36 | y |
C | 54 | 3 |
(1)求x、y;
(2)若从高校B相关的人中选2人作专题发言,应采用什么抽样法,请写出合理的抽样过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论: ①若x>0,则x>sinx恒成立;
②“若am2<bm2 , 则a<b”的逆命题为真命题
③m∈R,使f(x)=(m﹣1)x ![]() 是幂函数,且在(﹣∞,0)上单调递减
是幂函数,且在(﹣∞,0)上单调递减
④对于命题p:x∈R使得x2+x+1<0,则¬p:x∈R,均有x2+x+1>0
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系下,已知曲线C1:ρ=cosθ+sinθ和曲线C2:ρsin(θ﹣ ![]() )=
)= ![]() .
.
(1)求曲线C1和曲线C2的直角坐标方程;
(2)当θ∈(0,π)时,求曲线C1和曲线C2公共点的一个极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前55个圈中的●的个数是( )
A.10
B.9
C.8
D.11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com