已知二次函数f(x)=ax2+bx(a≠0,a、b为常数)满足f(1-x)=f(1+x),且方程f(x)=x有两相等实根
(1)求f(x)的解析式;
(2)在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的范围.
(3)是否存在实数m和n(m<n ),使f(x)的定义域和值域分别为[m,n]和[3m,3n],如果存在求出m和n的值.
【答案】
分析:(1)由f(1-x)=f(1+x),得函数的对称轴为x=1,又方程f(x)=x有两相等实根,即ax
2+(b-1)x=0有两相等实根,利用△=0可得关于a,b的方程,由此可求出a,b的值.
(2)区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,转化成二次函数在区间[-1,1]上恒为正,借助二次函数的性质转化即可求参数.
(3)本题主要是借助函数的单调性确定出函数在[m,n]上的单调性,找到区间中那个自变量的函数值是3m,3n,由此建立方程求解,若能解出值,说明存在,否则不存在.
解答: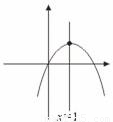
解:(1)∵f(1-x)=f(1+x)∴f(x)的对称轴为x=1即
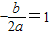
即b=-2a.
∵f(x)=x有两相等实根∴ax
2+bx=x即ax
2+(b-1)x=0有等根0,
∴b=1,
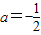
∴

(2)在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,
即

>2x+m在区间[-1,1]上恒成立
即x
2+2x+2m<0在区间[-1,1]上恒成立故有

解得m≤-

即当m≤-

时,在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方
(3)
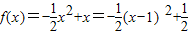
≤

故3n≤

,故m<n≤

又函数的对称轴为x=1,故f(x)在[m,n]单调递增则有
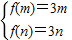
解得
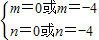
,又m<n,故m=-4,n=0
点评:本题考点是二次函数的性质考查综合利用函数的性质与图象转化解题,(1)中通过有相等的0根这一特殊性求参数;(2)中将函数图象的位置关系转化成了二次函数在区间上大于0恒成立的问题,借助函数的图象转化;(3)解法入手中最为巧妙,根据其图象开口向下这一性质,求出函数的最大值,利用最大值解出参数n的取值范围,从而结合对称轴为x=1得出函数在区间[m,n]单调性,得到方程组
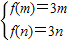
求参数,题后应好好总结每个小题的转化规律.

 解:(1)∵f(1-x)=f(1+x)∴f(x)的对称轴为x=1即
解:(1)∵f(1-x)=f(1+x)∴f(x)的对称轴为x=1即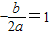 即b=-2a.
即b=-2a.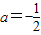

 >2x+m在区间[-1,1]上恒成立
>2x+m在区间[-1,1]上恒成立 解得m≤-
解得m≤-
 时,在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方
时,在区间[-1,1]上,y=f(x)的图象恒在y=2x+m的图象上方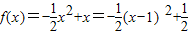 ≤
≤
 ,故m<n≤
,故m<n≤
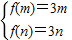
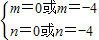 ,又m<n,故m=-4,n=0
,又m<n,故m=-4,n=0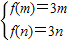 求参数,题后应好好总结每个小题的转化规律.
求参数,题后应好好总结每个小题的转化规律. 

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案