
已知ABCD-A1B1C1D1为正方体,①( +
+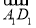 +
+ )2=3
)2=3 2;②
2;②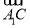 ·(
·(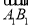 -
-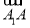 )=0;③向量
)=0;③向量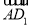 与向量
与向量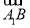 的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|
的夹角是60°;④正方体ABCD-A1B1C1D1的体积为| ·
·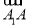 ·
·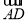 |.其中正确命题的序号是________.
|.其中正确命题的序号是________.
 综合自测系列答案
综合自测系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练7练习卷(解析版) 题型:解答题
如图,在△ABC中,∠ABC=90°,AB=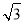 ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.
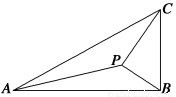
(1)若PB=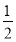 ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练16练习卷(解析版) 题型:选择题
直线4kx-4y-k=0与抛物线y2=x交于A,B两点,若|AB|=4,则弦AB的中点到直线x+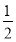 =0的距离等于( ).
=0的距离等于( ).
A. 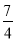 B.2 C.
B.2 C.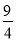 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练14练习卷(解析版) 题型:填空题
若直线l:4x+3y-8=0过圆C:x2+y2-ax=0的圆心且交圆C于A,B两点,O坐标原点,则△OAB的面积为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:解答题
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
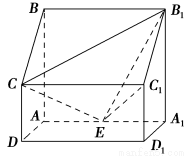
(1)证明B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练13练习卷(解析版) 题型:选择题
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
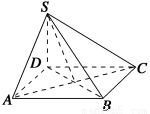
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练12练习卷(解析版) 题型:选择题
如图所示,在四边形A-BCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A?BCD,则在三棱锥ABCD中,下列命题正确的是( ).

A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练训练10练习卷(解析版) 题型:解答题
已知函数f(x)=(x-1)2,g(x)=4(x-1),数列{an}是各项均不为0的等差数列,其前n项和为Sn,点(an+1,S2n-1)在函数f(x)的图象上;数列{bn}满足b1=2,bn≠1,且(bn-bn+1)·g(bn)=f(bn)(n∈N+).
(1)求an并证明数列{bn-1}是等比数列;
(2)若数列{cn}满足cn=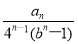 ,证明:c1+c2+c3+…+cn<3.
,证明:c1+c2+c3+…+cn<3.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习专题提升训练优化重组卷3练习卷(解析版) 题型:解答题
已知数列{an}的前n项和为Sn,且满足Sn=n2,数列{bn}满足bn= ,Tn为数列{bn}的前n项和.
,Tn为数列{bn}的前n项和.
(1)求数列{an}的通项公式an和Tn;
(2)若对任意的n∈N*,不等式λTn<n+(-1)n恒成立,求实数λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com