
【题目】如图,已知矩形ABCD中,AB=2,AD=1.将矩形沿对角线BD折起,使A移到点P,P在平面BCD上的投影O恰好落在CD边上.
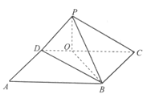
(1)证明:DP⊥平面BCP;
(2)求点O到平面PBD的距离.
【答案】(1)证明见解析(2)![]()
【解析】
(1)由已知可证BC⊥CD,DA⊥AB,由A点移动到了P点,可证PD⊥PB,过P点作PO⊥CD,利用PO⊥面BCD,可证BC⊥面PCD,利用线面垂直的性质得BC⊥PD,根据线面垂直的判定定理可证PD⊥面PBC.
(2)连接OB,由(1)可知DP⊥PC,可求PC,可证OP⊥CD,由DCPO=DPPC,解得OP,OC的值,可得S△ODB,设点O到平面PBD的距离为h,可得S△DPB=S△ABD=1,根据VP﹣DOB=VO﹣DPB,即可解得h的值.
(1)∵四边形ABCD为矩形,
∴BC⊥CD,DA⊥AB,
∵A点移动到了P点,
∴PD⊥PB,
又∵P点在平面BCD上的射影在CD上,
∴过P点作PO⊥CD,
∴PO⊥面BCD,
∴BC⊥面PCD,可得:BC⊥PD,
∴PD⊥面PBC,
(2)连接OB,由(1)可知DP⊥平面BCP,PC平面BCP,
所以DP⊥PC,
即PC![]() ,
,
由(1)可知OP⊥平面BCD,
而CD平面BCD,
所以OP⊥CD,
由DCPO=DPPC,解得:OP![]() ,
,
所以OC![]() ,
,
可得:OD![]() ,BD
,BD![]() ,sin∠ODB
,sin∠ODB![]() ,
,
可得S△ODB![]() sin∠ODB
sin∠ODB![]() ,
,
设点O到平面PBD的距离为h,可得S△DPB=S△ABD=1,
因为VP﹣DOB=VO﹣DPB,
所以![]() S△DOBPO
S△DOBPO![]() S△DPBh,
S△DPBh,
可得:![]() h,解得h
h,解得h![]() .
.
即点O到平面PBD![]() .
.


科目:高中数学 来源: 题型:
【题目】函数y=f(x)的导函数y=f′(x)的图象如图所示,给出下列命题:
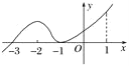
①-3是函数y=f(x)的极值点;
②-1是函数y=f(x)的最小值点;
③y=f(x)在区间(-3,1)上单调递增;
④y=f(x)在x=0处切线的斜率小于零.
以上正确命题的序号是( )
A. ①②B. ③④C. ①③D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x![]() |+|x﹣λ|,其中λ
|+|x﹣λ|,其中λ![]() .
.
(1)若对任意x∈R,恒有f(x)![]() ,求λ的最大值;
,求λ的最大值;
(2)在(1)的条件下,设λ的最大值为t,若正数m,n满足m+2n=mnt,求2m+n的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com