练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知集合A={x|2≤2x≤4}，B={x|0＜log2x＜2}，则A∪B=（ ）
    A.[1，4]
    B.[1，4）
    C.（1，2）
    D.[1，2]

    【答案】B
    【解析】解：由A中不等式变形得：21≤2x≤22，

    解得：1≤x≤2，即A=[1，2]，

    由B中不等式变形得：log21=0＜log2x＜2=log24，

    解得：1＜x＜4，即B=（1，4），

    则A∪B=[1，4），

    故选：B．

    【考点精析】关于本题考查的集合的并集运算和集合的交集运算，需要了解并集的性质：（1）AA∪B，BA∪B，A∪A=A，A∪=A,A∪B=B∪A;（2）若A∪B=B，则AB，反之也成立；交集的性质：（1）A∩BA，A∩BB，A∩A=A，A∩=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知实数x，y满足x2+y2﹣4x+6y+4=0，则 的最小值是（ ）
    A.2 +3
    B. ﹣3
    C. +3
    D. ﹣3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，四棱锥P﹣ABCD的底面ABCD是边长为1的菱形，∠BCD=60°，E是CD的中点，PA⊥底面ABCD，PA=2． （Ⅰ）证明：平面PBE⊥平面PAB；
    （Ⅱ）求二面角B﹣PE﹣D的余弦值．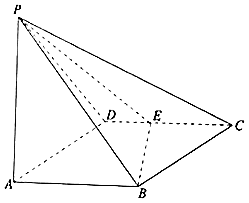

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若圆C1：（x﹣1）2+（y+3）2=1与圆C2：（x﹣a）2+（y﹣b）2=1外离，过直线l：x﹣y﹣1=0上任意一点P分别做圆C1 ， C2的切线，切点分别为M，N，且均保持|PM|=|PN|，则a+b=（ ）
    A.﹣2
    B.﹣1
    C.1
    D.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地区有小学21所，中学14所，大学7所，现采用分层抽样的方法从这些学校中抽取6所学校对学生进行视力调查．
    （1）求应从小学、中学、大学中分别抽取的学校数目；
    （2）若从抽取的6所学校中随机抽取2所学校做进一步数据分析． （ⅰ）列出所有可能的抽取结果；
    （ⅱ）求抽取的2所学校均为小学的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足（an+1﹣1）（an﹣1）=3（an﹣an+1），a1=2，令bn= ．
    （1）求数列{bn}的通项公式；
    （2）求数列{bn3n}的前n项和Sn ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体ABCD﹣A1B1C1D1中，点O为线段BD的中点，设点P在线段CC1上，直线OP与平面A1BD所成的角为α，则sinα的取值范围是（ ）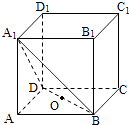
    A.[ ，1]
    B.[ ，1]
    C.[ ， ]
    D.[ ，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某种零件按质量标准分为1，2，3，4，5五个等级，现从批该零件中随机抽取20个，对其等级进行统计分析，得到频率分布表如下：

    等级

    1

    2

    3

    4

    5

    频率

    0.05

    m

    0.15

    0.35

    n


    （1）在抽取的20个零件中，等级为5的恰有2个，求m，n的值；
    （2）在（1）的条件下，从等级为3和5的所有零件中，任意抽取2个，求抽取的2个零件等级不相同的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（）在处的切线与轴平行.

    （1）讨论在上的单调性；

    （2）设， ，证明： .

    查看答案和解析>>

    同步练习册答案