练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．求$\underset{lim}{x→0}$（$\frac{1}{x}$-cotx）．

    分析 利用洛必达法化简$\underset{lim}{x→0}$（$\frac{1}{x}$-cotx）=$\underset{lim}{x→0}$（$\frac{sinx-xcosx}{xsinx}$）=$\underset{lim}{x→0}$$\frac{cosx-cosx+xsinx}{sinx+xcosx}$=$\underset{lim}{x→0}$$\frac{sinx+xcosx}{cosx+cosx-xsinx}$=0．

    解答 解：$\underset{lim}{x→0}$（$\frac{1}{x}$-cotx）
    =$\underset{lim}{x→0}$（$\frac{1}{x}$-$\frac{cosx}{sinx}$）
    =$\underset{lim}{x→0}$（$\frac{sinx-xcosx}{xsinx}$）
    =$\underset{lim}{x→0}$$\frac{cosx-cosx+xsinx}{sinx+xcosx}$
    =$\underset{lim}{x→0}$$\frac{xsinx}{sinx+xcosx}$
    =$\underset{lim}{x→0}$$\frac{sinx+xcosx}{cosx+cosx-xsinx}$=0．

    点评 本题考查了导数的运算的应用及洛必达法则的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

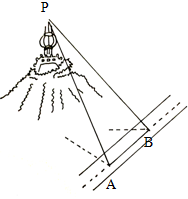    18．沿着山边一条平直的公路测量山顶一建筑物的高度，如图所示，已知A处测量建筑物顶部的仰角为60°，B处测量建筑物顶部的仰角为30°，已知图中
    PA⊥AB，AB=$\frac{440\sqrt{6}}{3}$米，山的高度是190米，则建筑物的高度为30 米．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．函数$f（x）={log_3}x-{（\frac{1}{2}）^x}$，若实数x0是函数f（x）的零点，且0＜x1＜x0，则f（x1）的值为（　　）
    A．恒为正B．等于零C．恒为负D．不小于零

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知函数f（x）=$\frac{x+a}{x+b}$，a＞b＞0，判断f（x）在（-b，+∞）上的单调性，并证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．图中阴影部分所表示的集合是（　　）
    A．（A∪B）∪（B∪C）B．[∁U（A∩C）]∪BC．（A∪C）∩（∁UB）D．B∩[∁U（A∪C）]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知数列：{an}满足（2n+1）an=（2n-1）an+1（n∈N*），且a1=1．
    （1）求证：数列{an}为等差数列；
    （2）设bn=$\frac{1}{{a}_{n}{a}_{n+1}}$求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．某工厂平均每天生产某种机器零件大约10000件，要求产品检验员每天抽取50件零件，检查其质量状况，采用系统抽样方法抽取，若抽取的第一组中的号码为0010，则第三组抽取的号码为0410．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．设P是椭圆$\frac{x^2}{4}+\frac{y^2}{9}=1$上的点，若F1，F2是椭圆的两个焦点，则|PF1|+|PF2|等于（　　）
    A．4B．8C．6D．18

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．某企业有4个分厂，新培训了一批6名技术人员，将这6名技术人员分配到各分厂，要求每个分厂至少1人，则不同的分配方案种数为（　　）
    A．1080B．480C．1560D．300

    查看答案和解析>>

    同步练习册答案