
【题目】某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在![]() .
.
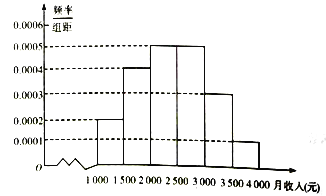
(1)求居民收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数、平均数及其众数;
(3)为了分析居民的收入与年龄、职业等方面的关系,从这10000人中用分层抽样方法抽出100人作进一步分析,则应月收入为![]() 的人中抽取多少人?
的人中抽取多少人?
科目:高中数学 来源: 题型:
【题目】某企业开发一种新产品,现准备投入适当的广告费,对产品进行促销,在一年内,预计年销量Q(万件)与广告费x(万件)之间的函数关系为![]() ,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为
,已知生产此产品的年固定投入为3万元,每年产1万件此产品仍需要投入32万元,若年销售额为![]() ,而当年产销量相等。
,而当年产销量相等。
(1)试将年利润P(万件)表示为年广告费x(万元)的函数;
(2)当年广告费投入多少万元时,企业年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先后2次抛掷一枚骰子,将得到的点数分别记为![]() .
.
(Ⅰ)求满足![]() 的概率;
的概率;
(Ⅱ)设三条线段的长分别为![]() 和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
和5,求这三条线段能围成等腰三角形(含等边三角形)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 两点的坐标分别为
两点的坐标分别为![]() ,动点
,动点![]() 满足:直线
满足:直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 作两条互相垂直的射线,与(1)的轨迹分别交于
作两条互相垂直的射线,与(1)的轨迹分别交于![]() 两点,求
两点,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,cos C=.
(1)若·=,求c的最小值;
(2)设向量x=(2sin B,-),y=,且x∥y,求sin(B-A)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于![]() ,抛物线
,抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则抛物线
的右焦点重合,则抛物线![]() 上的动点
上的动点![]() 到直线
到直线![]() 和
和![]() 的距离之和的最小值为__________.
的距离之和的最小值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图, 椭圆![]() 的离心率是
的离心率是![]() ,点
,点![]() 在椭圆上, 设点
在椭圆上, 设点![]() 分别是椭圆的右顶点和上顶点, 过 点
分别是椭圆的右顶点和上顶点, 过 点![]() 引椭圆
引椭圆![]() 的两条弦
的两条弦![]() 、
、![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与
与![]() 的斜率是互为相反数.
的斜率是互为相反数.
①直线![]() 的斜率是否为定值?若是求出该定值, 若不是,说明理由;
的斜率是否为定值?若是求出该定值, 若不是,说明理由;
②设![]() 、
、![]() 的面积分别为
的面积分别为![]() 和
和![]() ,求
,求![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中,![]() ,
,![]() ,
,![]() ,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且
,A为PD的中点,如图.将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,且![]() ,如图.
,如图.
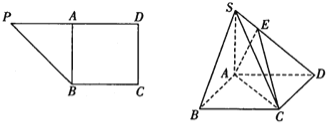
(Ⅰ)求证:SA⊥平面ABCD;
(Ⅱ)求二面角E﹣AC﹣D的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com