


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:
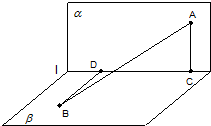 (2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,
(2006•广州一模)如图,长度为2的线段AB夹在直二面角α-l-β的两个半平面内,A∈α,B∈β,查看答案和解析>>
科目:高中数学 来源: 题型:
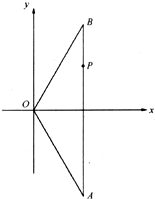 (2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.
(2006•广州一模)如下图,在△OAB中,|OA|=|OB|=4,点P分线段AB所成的比为3:1,以OA、OB所在直线为渐近线的双曲线M恰好经过点P,且离心率为2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com