
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 存在两个极值点
存在两个极值点![]() ,
,![]() ,且
,且![]() ,证明:
,证明:![]() .
.
【答案】(1)答案见解析;(2)证明见解析.
【解析】分析:(1)对m分类讨论求函数![]() 的单调区间.(2)先求出
的单调区间.(2)先求出![]() ,再构造函数
,再构造函数![]() ,
,![]() ,求它的范围.
,求它的范围.
详解:(1)函数![]() 定义域为
定义域为![]() ,且
,且![]() ,
,![]() ,
,
令![]() ,
,![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 上单调递减;
上单调递减;
当![]() ,即
,即![]() 时,由
时,由![]() ,解得
,解得![]() ,
,![]() ,
,
若![]() ,则
,则![]() ,∴
,∴![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
若![]() ,则
,则![]() ,∴
,∴![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
综上所述:![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;
;
![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() ,单调递增区间为
,单调递增区间为![]() ;
;
![]() 时,
时,![]() 的单调递减区间为
的单调递减区间为![]() .
.
(2)因为函数![]() 定义域为
定义域为![]() ,且
,且![]() ,
,
∵函数![]() 存在两个极值点,∴
存在两个极值点,∴![]() 在
在![]() 上有两个不等实根
上有两个不等实根![]() ,
,![]() ,
,
记![]() ,则
,则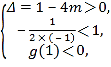 ∴
∴![]() ,
,
从而由![]() 且
且![]() ,可得
,可得![]() ,
,![]() ,
,
∴![]()
![]() ,
,
构造函数![]() ,
,![]() ,
,
则![]() ,
,
记![]() ,
,![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() (
(![]() ,故舍去),
,故舍去),
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
又![]() ,
,![]() ,
,
∴当![]() 时,恒有
时,恒有![]() ,即
,即![]() ,
,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() ,
,
∴![]() .
.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2α﹣4cosα=0.已知直线l的参数方程为![]() (
(![]() 为参数),点M的直角坐标为
为参数),点M的直角坐标为![]() .
.
(1)求直线l和曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站登录密码由四位数字组成,某同学将四个数字0,3,2,5,编排了一个顺序作为密码.由于长时间未登录该网站,他忘记了密码.若登录时随机输入由0,3,2,5组成的一个密码,则该同学不能顺利登录的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,过
,过![]() 上一动点
上一动点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() .当点
.当点![]() 满足
满足![]() 时,点
时,点![]() 的轨迹
的轨迹![]() 恰是一个圆.
恰是一个圆.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若与曲线![]() 切于
切于![]() 点的直线
点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且当
两点,且当![]() 轴时,
轴时,![]() ,求
,求![]() 的最大面积.
的最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求直线
,求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润![]() 与时间
与时间![]() 的关系,可选用
的关系,可选用
A.一次函数B.二次函数
C.指数型函数D.对数型函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com