
分析 (1)判断数列{$\frac{{a}_{n}}{n}$}是等差数列,然后求解通项公式.
(2)利用错位相减法求解数列的和即可.
解答 (本小题12分)
(1)解:由已知可得$\frac{{a}_{n}+1}{n+1}$-$\frac{{a}_{n}}{n}$=1,….(2分)
所以是以$\frac{{a}_{1}}{1}$=1为首项,1为公差的等差数列.得$\frac{{a}_{n}}{n}$=1+(n-1)•1=n,
所以an=n2,…(4分)
(2)由(1)得an=n2,从而bn=n•3n….(5分)
Sn=1×31+2×32+3×33+…+n•3n①
3Sn=1×32+2×33+3×34+…+(n-1)•3n+n•3n+1②
①-②得:-2Sn=31+32+33+…+3n-n•3n+1
=$\frac{(1-2n)?3^{n+1}-3}{2}$.….(10分)
所以Sn=$\frac{(2n-1)•3^{n+1}+3}{4}$.….(12分)
点评 本题考查数列的通项公式的应用,数列求和的方法,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
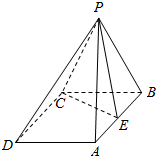 如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,PA=PB,且侧面PAB⊥平面ABCD,点E是棱AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com