练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本题满分14分）定义：对于函数,.若对定义域内的恒成立,则称函数为函数.(1)请举出一个定义域为的函数,并说明理由;(2)对于定义域为的函数，求证：对于定义域内的任意正数，均有;

    (3)对于值域的函数,求证：.

    (Ⅰ)    (Ⅱ)见解析   （Ⅲ）见解析


    解析:

    （1）如函数就是定义域内的函数.

    下面进行证明: 必定成立.

    （2）构造函数，，

    即在R上递增所以，

    ，…

    得到，，

    …

    相加后，得到：

    （3）构造函数，则，因为，所以

         得到有

         所以，…，

         所以有

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2011年甘肃省高一上学期期中考试数学 题型：解答题

    （本题满分14分）某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时，可全部租出.当每辆车的月租金每增加50元时，未租出的车将会增加一辆.租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元.

    （1）当每辆车的月租金定为3600元时，能租出多少辆车？

    （2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年江西省六校高三联考数学理卷 题型：解答题

    （（本题满分14分）

    已知椭圆的两个焦点，且椭圆短轴的两个端点与构成正三角形．

    （1）求椭圆的方程；

    （2）过点（1，0）且与坐标轴不平行的直线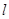与椭圆交于不同两点P、Q，若在轴上存在定点E（，0），使恒为定值，求的值.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年广东省惠州市高三第三次调研考试数学文卷 题型：解答题

    （本题满分14分）

    已知动圆过定点，且与定直线相切.

    （1）求动圆圆心的轨迹的方程；

    （2）若是轨迹的动弦，且过， 分别以、为切点作轨迹的切线，设两切线交点为，证明:.

     

    查看答案和解析>>

    科目：高中数学 来源：2013届广东省高二第一学期期末考试文科数学 题型：解答题

    （本题满分14分）

    已知动圆过定点P(1,0)且与定直线相切,点C在上.

    （Ⅰ）求动圆圆心M的轨迹方程;

    （Ⅱ）设过点P且斜率为的直线与曲线交于A、B两点.问直线上是否存在点C ,使得是以为直角的直角三角形？如果存在，求出点C的坐标;若不能,请说明理由.

     

     

    查看答案和解析>>

    同步练习册答案