
分析 由韦达定理和一元二次方程根的存在性可得cosθ的范围,结合余弦函数的图象可得.
解答 解:∵α,β是关于x的方程x2+2(cosθ+1)x+cos2θ=0的两个根,
∴△=4(cosθ+1)2-4(cosθ)2≥0,解得cosθ≥-$\frac{1}{2}$ ①
由韦达定理得α+β=-2(cosθ+1),αβ=cos2θ,
由|α-β|≤2$\sqrt{2}$可得(α-β)2≤8,即(α+β)2-4αβ≤8,
代入可得4(cosθ+1)2-4(cosθ)2≤8,解得cosθ≤$\frac{1}{2}$ ②
由①②得-$\frac{1}{2}$≤cosθ≤$\frac{1}{2}$,
∴$\frac{π}{3}$+2kπ≤θ≤$\frac{2π}{3}$+2kπ或$\frac{4π}{3}$+2kπ≤θ≤$\frac{5π}{3}$+2kπ(k∈Z).
故角θ的集合为{θ|$\frac{π}{3}$+kπ≤θ≤$\frac{2π}{3}$+kπ,k∈Z}
点评 本题考查三角函数恒等变换,涉及一元二次方程根与系数关系和三角函数的性质,属中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:选择题
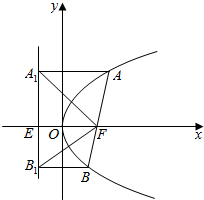 如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )
如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com