
【题目】在锐角三角形ABC中,9tanAtanB+tanBtanC+tanCtanA的最小值为 .
【答案】25
【解析】解:如图,不妨设CD=1,AD=m,BD=n,
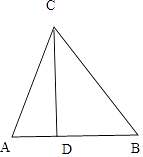
∴tanA= ![]() ,tanB=
,tanB= ![]() ,(m>0,n>0),
,(m>0,n>0),
∴tanC=![]() tan(A+B)=
tan(A+B)=![]()
![]() =
= ![]() ,
,
∵tanC>0,
∴mn<1,
∴9tanAtanB+tanBtanC+tanCtanA= ![]() +(
+( ![]() +
+ ![]() )
) ![]() ,
,
= ![]() +
+ ![]() ,
,
≥ ![]() +
+ ![]() ,
,
=( ![]() +
+ ![]() )[mn+(1﹣mn)],
)[mn+(1﹣mn)],
=9+4+ ![]() +
+ ![]() ,
,
≥13+2 ![]()
=13+12=25,当且仅当 ![]() =
= ![]() ,即m=n=
,即m=n= ![]() 时取等号,
时取等号,
故最小值为25,
所以答案是:25 .
【考点精析】本题主要考查了基本不等式在最值问题中的应用的相关知识点,需要掌握用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、三相等”才能正确解答此题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】设△ABC的三个内角分别为A,B,C.向量 ![]() 共线. (Ⅰ)求角C的大小;
共线. (Ⅰ)求角C的大小;
(Ⅱ)设角A,B,C的对边分别是a,b,c,且满足2acosC+c=2b,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(a2﹣3a+3)ax是指数函数,
(1)求f(x)的表达式;
(2)判断F(x)=f(x)﹣f(﹣x)的奇偶性,并加以证明
(3)解不等式:loga(1﹣x)>loga(x+2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于给定的正整数k,如果各项均为正数的数列{an}满足:对任意正整数n(n>k),an﹣kan﹣k+1…an﹣1an+1…an+k﹣1an+k=an2k总成立,那么称{an}是“Q(k)数列”.
(1)若{an}是各项均为正数的等比数列,判断{an}是否为“Q(2)数列”,并说明理由;
(2)若{an}既是“Q(2)数列”,又是“Q(3)数列”,求证:{an}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为函数y=f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)图象的一部分,其中点 ![]() 是图象的一个最高点,点
是图象的一个最高点,点 ![]() 是与点P相邻的图象与x轴的一个交点.
是与点P相邻的图象与x轴的一个交点.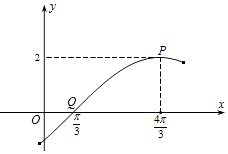
(1)求函数f(x)的解析式;
(2)若将函数f(x)的图象沿x轴向右平移 ![]() 个单位,再把所得图象上每一点的横坐标都变为原来的
个单位,再把所得图象上每一点的横坐标都变为原来的 ![]() (纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的单调递增区间.
(纵坐标不变),得到函数y=g(x)的图象,求函数y=g(x)的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,底面
中,底面 ![]() 是菱形,
是菱形, ![]() ,
, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
是 ![]() 中点.
中点.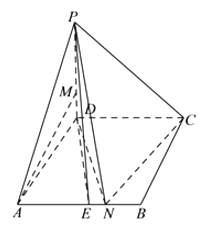
(I)求证:直线 ![]() 平面
平面 ![]() .
.
(II)求证:直线 ![]() 平面
平面 ![]() .
.
(III)在 ![]() 上是否存在一点
上是否存在一点 ![]() ,使得二面角
,使得二面角 ![]() 的大小为
的大小为 ![]() ,若存在,确定
,若存在,确定 ![]() 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ﹣
﹣ ![]() +cx+d有极值.
+cx+d有极值.
(Ⅰ)求实数c的取值范围;
(Ⅱ)若f(x)在x=2处取得极值,且当x<0时,f(x)< ![]() +2d恒成立,求实数d的取值范围.
+2d恒成立,求实数d的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com