
【题目】张先生知道清晨从甲地到乙地有好、中、差三个班次的客车.但不知道具体谁先谁后.他打算:第一辆看后一定不坐,若第二辆比第一辆舒服,则乘第二辆;否则坐第三辆.问张先生坐到好车的概率和坐到差车的概率分别是( )
A.![]() 、
、 ![]()
B.![]() 、
、 ![]()
C.![]() 、
、 ![]()
D.![]() 、
、 ![]()
【答案】C
【解析】解:设三辆车的等次为:下 中 上,它们的先后次序分下列6种情况, 下 中 上 他乘上中等车
下 上 中 他乘上上等车
中 下 上 他乘上上等车
中 上 下 他乘上上等车
上 下 中 他乘上中等车
上 中 下 他乘上下等车
他乘上上等车的情况数为:3
那么他乘上上等车的概率为 ![]()
他乘上下等车的情况数为:1
那么他乘上下等车的概率为 ![]() .
.
故选C.
本题考查的知识点是古典概型,设三辆车的等次为:下 中 上,我们分6种情况,下 中 上 他没乘上上等车;下 上 中 他乘上上等车;中 下 上 他乘上上等车;中 上 下 他乘上上等车;上 下 中 他没乘上上等车;上 中 下 他没乘上上等车;一共6种情形,然后代入古典概型公式计算,即可得到答案.


科目:高中数学 来源: 题型:
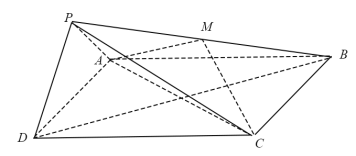
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD//平面MAC,PA=PD=![]() ,AB=4.
,AB=4.
(I)求证:M为PB的中点;
(II)求二面角B-PD-A的大小;
(III)求直线MC与平面BDP所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2bx+c,且f(1)=f(3)=﹣1.设a>0,将函数f(x)的图像先向右平移a个单位长度,再向下平移a2个单位长度,得到函数g(x)的图像. (Ⅰ)若函数g(x)有两个零点x1 , x2 , 且x1<4<x2 , 求实数a的取值范围;
(Ⅱ)设连续函数在区间[m,n]上的值域为[λ,μ],若有 ![]() ,则称该函数为“陡峭函数”.若函数g(x)在区间[a,2a]上为“陡峭函数”,求实数a的取值范围.
,则称该函数为“陡峭函数”.若函数g(x)在区间[a,2a]上为“陡峭函数”,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P﹣ABCD中,底面ABCD是棱长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC中点,若H为PD上的动点,EH与平面PAD所成最大角的正切值为 ![]() .
. 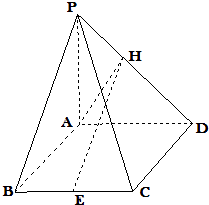
(1)当EH与平面PAD所成角的正切值为 ![]() 时,求证:EH∥平面PAB;
时,求证:EH∥平面PAB;
(2)在(1)的条件下,求二面角A﹣PB﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(2)班共有60名同学参加期末考试,现将其数学学科成绩(均为整数)分成六个分数段[40,50),[50,60),…,[90,100],画出如如图所示的部分频率分布直方图,请观察图形信息,回答下列问题: 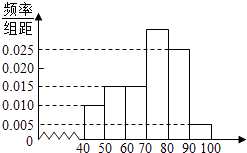
(1)求70~80分数段的学生人数;
(2)估计这次考试中该学科的优分率(80分及以上为优分)、中位数、平均值;
(3)现根据本次考试分数分成下列六段(从低分段到高分段依次为第一组、第二组、…、第六组)为提高本班数学整体成绩,决定组与组之间进行帮扶学习.若选出的两组分数之差大于30分(以分数段为依据,不以具体学生分数为依据),则称这两组为“最佳组合”,试求选出的两组为“最佳组合”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)记 ,设
,设![]() ,
, ![]() 为函数
为函数![]() 图象上的两点,且
图象上的两点,且![]() .
.
(ⅰ)当![]() ,
, ![]() 时,若
时,若![]() 在
在![]() 处的切线相互垂直,求证:
处的切线相互垂直,求证: ![]() ;
;
(ⅱ)若![]() 在点
在点![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆![]() 的左、右焦点分别为F1,F2,离心率为
的左、右焦点分别为F1,F2,离心率为![]() ,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
,两准线之间的距离为8.点P在椭圆E上,且位于第一象限,过点F1作直线PF1的垂线l1,过点F2作直线PF2的垂线l2.
(1)求椭圆E的标准方程;
(2)若直线l1,l2的交点Q在椭圆E上,求点P的坐标.
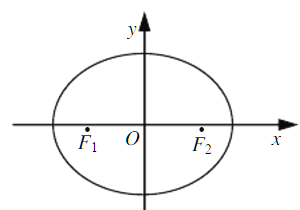
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com