
【题目】已知函数f(x)= 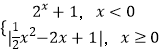 ,方程f2(x)﹣af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
,方程f2(x)﹣af(x)+b=0(b≠0)有六个不同的实数解,则3a+b的取值范围是( )
A.[6,11]
B.[3,11]
C.(6,11)
D.(3,11)
科目:高中数学 来源: 题型:
【题目】已知全集U=R,集合A={x|x2+x>0},集合B= ![]() ,则(UA)∪B=( )
,则(UA)∪B=( )
A.[0,2)
B.[﹣1,0]
C.[﹣1,2)
D.(﹣∞,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() x3﹣(1+
x3﹣(1+ ![]() )x2+2bx在区间[3,5]上不是单调函数,则函数f(x)在R上的极大值为( )
)x2+2bx在区间[3,5]上不是单调函数,则函数f(x)在R上的极大值为( )
A.![]() b2﹣
b2﹣ ![]() b3
b3
B.![]() b﹣
b﹣ ![]()
C.0
D.2b﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD-A1B1C1D1为正方体,下面结论错误的是 ( )
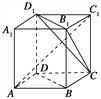
A. BD∥平面CB1D1 B. AC1⊥BD
C. AC1⊥平面CB1D1 D. 异面直线AD与CB1所成的角为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣(2a+1)x+lnx(a∈R) (Ⅰ)当a>0时,求函数f(x)的单调区间;
(Ⅱ)设g(x)=f(x)+2ax,若g(x)有两个极值点x1 , x2 , 且不等式g(x1)+g(x2)<λ(x1+x2)恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直角梯形ACDE所在的平面垂直于平面ABC,∠BAC=
∠ACD=90°,∠EAC=60°,AB=AC=AE.
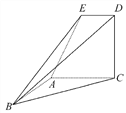
(1)在直线BC上是否存在一点P,使得DP∥平面EAB?请证明你的结论.
(2)求平面EBD与平面ABC所成的锐二面角θ的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一个矩形花园里需要铺两条笔直的小路,已知矩形花园长AD=5m,宽AB=3m,其中一条小路定为AC,另一条小路过点D,问如何在BC上找到一点M,使得两条小路AC与DM相互垂直?
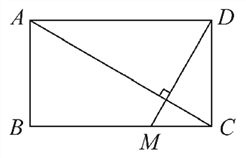
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中,给出以下四个结论:
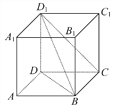
①D1C∥平面A1ABB1;②A1D1与平面BCD1相交;
③AD⊥平面D1DB;④平面BCD1⊥平面A1ABB1.
其中正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了保护学生的视力,教室内的日光灯在使用一段时间后必须更换.已知某校使用的100只日光灯在必须换掉前的使用天数如下表:
天数/天 | 151~180 | 181~210 | 211~240 | 241~270 | 271~300 | 301~330 | 331~360 | 361~390 |
灯管数/只 | 1 | 11 | 18 | 20 | 25 | 16 | 7 | 2 |
(1)试估计这种日光灯的平均使用寿命;
(2)若定期更换,可选择多长时间统一更换合适?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com