
【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
,![]() 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.
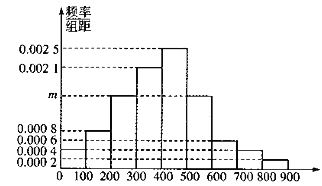
(1)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用![]() 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
【答案】(Ⅰ)![]() ,中位数为408度.(Ⅱ)
,中位数为408度.(Ⅱ)![]() ,分布列见解析.
,分布列见解析.
【解析】试题分析: (Ⅰ)根据频率分布直方图中小长方形面积等于对应区间概率,而所有概率和为1,列出方程,解出![]() 的值;因为中位数对应概率为
的值;因为中位数对应概率为![]() ,所以先估计中位数所在区间,再根据概率为
,所以先估计中位数所在区间,再根据概率为![]() ,列方程,解出中位数,(Ⅱ)先根据频数等于总数与概率的乘积得200户居民月均用电量在
,列方程,解出中位数,(Ⅱ)先根据频数等于总数与概率的乘积得200户居民月均用电量在![]() 度的户数是8,月均用电量在
度的户数是8,月均用电量在![]() 度的户数是4.再确定随机变量的取法,利用组合数分别计算对应的概率,列表可得分布列,最后根据数学期望公式求期望.
度的户数是4.再确定随机变量的取法,利用组合数分别计算对应的概率,列表可得分布列,最后根据数学期望公式求期望.
试题解析:解:(Ⅰ)![]() ,
,
∴![]() .
.
设中位数是![]() 度,前5组的频率之和为
度,前5组的频率之和为![]() ,
,
而前4组的频率之和为![]() ,
,
所以![]() ,
,![]() ,
,
故![]() ,即居民月均用电量的中位数为408度.
,即居民月均用电量的中位数为408度.
(Ⅱ)200户居民月均用电量在![]() 度的户数是8,月均用电量在
度的户数是8,月均用电量在![]() 度的户数是4.
度的户数是4.
故随机变量![]() 的取值为0,1,2,3,4,且
的取值为0,1,2,3,4,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以随机变量![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
故![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】一企业从某条生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到如下的频率分布表:
x | [11,13) | [13,15) | [15,17) | [17,19) | [19,21) | [21,23) |
频数 | 2 | 12 | 34 | 38 | 10 | 4 |
(Ⅰ)作出样本的频率分布直方图,并估计该技术指标值x的平均数和众数;
(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系下,已知曲线C1:ρ=cosθ+sinθ和曲线C2:ρsin(θ-![]() )=
)=![]() .
.
(1)求曲线C1和曲线C2的直角坐标方程;
(2)当θ∈(0,π)时,求曲线C1和曲线C2公共点的一个极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】沪昆高速铁路全线2016年12月28日开通运营.途经鹰潭北站的![]() 、
、![]() 两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了月乘车次数的频率分布直方图和频数分布表.
两列列车乘务组工作人员为了了解乘坐本次列车的乘客每月需求情况,分别在两个车次各随机抽取了100名旅客进行调查,下面是根据调查结果,绘制了月乘车次数的频率分布直方图和频数分布表.
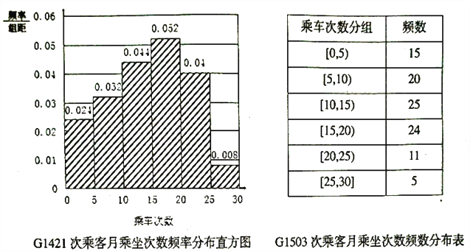
(1)若将频率视为概率,月乘车次数不低于15次的称之为“老乘客”,试问:哪一车次的“老乘客”较多,简要说明理由;
(2)已知在![]() 次列车随机抽到的50岁以上人员有35名,其中有10名是“老乘客”,由条件完成
次列车随机抽到的50岁以上人员有35名,其中有10名是“老乘客”,由条件完成![]() 列联表,并根据资料判断,是否有
列联表,并根据资料判断,是否有![]() 的把握认为年龄与乘车次数有关,说明理由.
的把握认为年龄与乘车次数有关,说明理由.
老乘客 | 新乘客 | 合计 | |
50岁以上 | |||
50岁以下 | |||
合计 |
附:随机变量![]() (其中
(其中![]() 为样本容量)
为样本容量)
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=x![]() (m∈N*).
(m∈N*).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若该函数还经过点(2, ![]() ),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“幸”“福”“快”“乐”四个字,有放回地从中任取一个小球,取到“快”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止的概率为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在区间
是定义在区间![]() 上的奇函数,且
上的奇函数,且![]() 若对于任意的
若对于任意的![]() 有
有![]()
(1)判断并证明函数的单调性;
(2)解不等式![]() ;
;
(3)若![]() 对于任意的
对于任意的![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是(-∞,+∞)上的奇函数,且f(x)的图象关于x=1对称,当x∈[0,1]时,f(x)=2x-1.
(1)当x∈[1,2]时,求f(x)的解析式;
(2)计算f(0)+f(1)+f(2)+…+f(2017)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩掷骰子游戏,甲掷出的点数记为![]() ,乙掷出的点数记为
,乙掷出的点数记为![]() ,
,
若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根时甲胜;方程有
有两个不相等的实数根时甲胜;方程有
两个相等的实数根时为“和”;方程没有实数根时乙胜.
(1)列出甲、乙两人“和”的各种情形;
(2)求甲胜的概率.
必要时可使用此表格

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com