
【题目】若函数![]() (
(![]() 是自然对数的底数)在
是自然对数的底数)在![]() 的定义域上单调递增,则称函数
的定义域上单调递增,则称函数![]() 具有
具有![]() 性质.下列函数中所有具有
性质.下列函数中所有具有![]() 性质的函数的序号为( )
性质的函数的序号为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】AD
【解析】
利用指数函数的性质与导数知识逐一判断新函数的单调性即可.
解:对于A,f(x)=2﹣x,则g(x)=exf(x)=ex2﹣x=(![]() )x为实数集上的增函数;
)x为实数集上的增函数;
对于B,f(x)=3﹣x,则g(x)=exf(x)=ex3﹣x=(![]() )x为实数集上的减函数;
)x为实数集上的减函数;
对于C,f(x)=x3,则g(x)=exf(x)=exx3,
g′(x)=exx3+3exx2=ex(x3+3x2)=exx2(x+3),当x<﹣3时,g′(x)<0,
∴g(x)=exf(x)在定义域R上先减后增;
对于D,f(x)=x2+2,则g(x)=exf(x)=ex(x2+2),
g′(x)=ex(x2+2)+2xex=ex(x2+2x+2)>0在实数集R上恒成立,
∴g(x)=exf(x)在定义域R上是增函数.
故选:AD.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,椭圆的离心率为
,椭圆的离心率为![]() ,过椭圆
,过椭圆![]() 的左焦点
的左焦点![]() ,且斜率为
,且斜率为![]() 的直线
的直线![]() ,与以右焦点
,与以右焦点![]() 为圆心,半径为
为圆心,半径为![]() 的圆
的圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)线段![]() 是椭圆
是椭圆![]() 过右焦点
过右焦点![]() 的弦,且
的弦,且![]() ,求
,求![]() 的面积的最大值以及取最大值时实数
的面积的最大值以及取最大值时实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
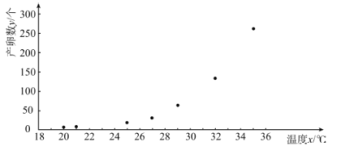
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为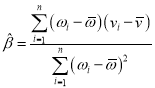 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
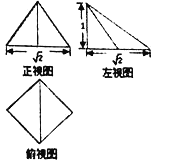
【题目】刘徽《九章算术商功》中将底面为长方形,两个三角面与底面垂直的四棱锥体叫做阳马.如图,是一个阳马的三视图,则其外接球的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱载堉(1536—1611),明太祖九世孙,音乐家、数学家、天文历算家,在他多达百万字的著述中以《乐律全书》最为著名,在西方人眼中他是大百科全书式的学者王子。他对文艺的最大贡献是他创建了“十二平均律”,此理论被广泛应用在世界各国的键盘乐器上,包括钢琴,故朱载堉被誉为“钢琴理论的鼻祖”。“十二平均律”是指一个八度有13个音,相邻两个音之间的频率之比相等,且最后一个音频率是最初那个音频率的2倍,设第二个音的频率为![]() ,第八个音的频率为
,第八个音的频率为![]() ,则
,则![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
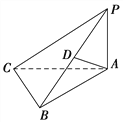
【题目】如图所示,在三棱锥P–ABC中,PA⊥平面ABC,D是棱PB的中点,已知PA=BC=2,AB=4,CB⊥AB,则异面直线PC,AD所成角的余弦值为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
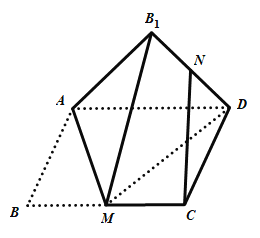
A.存在某个位置,使得![]()
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]()
D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,函数
,函数![]() ,
,![]() ,其中
,其中![]() 为常数,且
为常数,且![]() ,令函数
,令函数![]() 为函数
为函数![]() 和
和![]() 的积函数.
的积函数.
(1)求函数![]() 的表达式,并求其定义域;
的表达式,并求其定义域;
(2)当![]() 时,求函数
时,求函数![]() 的值域
的值域
(3)是否存在自然数![]() ,使得函数
,使得函数![]() 的值域恰好为
的值域恰好为![]() ?若存在,试写出所有满足条件的自然数
?若存在,试写出所有满足条件的自然数![]() 所构成的集合;若不存在,试说明理由.
所构成的集合;若不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com