
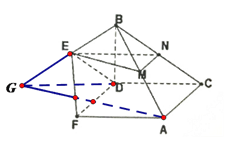
【题目】如图几何体中,矩形![]() 所在平面与梯形
所在平面与梯形![]() 所在平面垂直,且
所在平面垂直,且![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)证明: ![]() 平面
平面![]() ;
;
(2)证明: ![]() 平面
平面![]() .
.
科目:高中数学 来源: 题型:
【题目】从孝感地区中小学生中抽取部分学生,进行肺活量调查.经了解,该地区小学、初中、高中三个学段学生的肺活量有较大差异,而同一学段男女生的肺活量差异不大.在下面的抽样方法中,最合理的抽样方法是( )
A. 简单的随机抽样 B. 按性别分层抽样 C. 按学段分层抽样 D. 系统抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题一定正确的是( )
A. 三点确定一个平面 B. 依次首尾相接的四条线段必共面
C. 直线与直线外一点确定一个平面 D. 两条直线确定一个平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小型餐馆一天中要购买![]() ,
,![]() 两种蔬菜,
两种蔬菜,![]() ,
,![]() 蔬菜每公斤的单价分别为2元和3元.根据需要
蔬菜每公斤的单价分别为2元和3元.根据需要![]() 蔬菜至少要买6公斤,
蔬菜至少要买6公斤,![]() 蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,
蔬菜至少要买4公斤,而且一天中购买这两种蔬菜的总费用不能超过60元.如果这两种蔬菜加工后全部卖出,![]() ,
,![]() 两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
两种蔬菜加工后每公斤的利润分别为2元和1元,餐馆如何采购这两种蔬菜使得利润最大,利润最大为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样一道题:把120个面包分成5份,使每份的面包数成等差数列,且较多的三份之和恰好是较少的两份之和的7倍,则最少的那份有( )个面包.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直三棱柱![]() 的底面为正三角形,
的底面为正三角形,![]() 分别是
分别是![]() 的中点.
的中点.
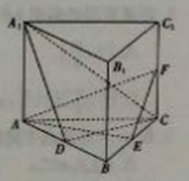
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 中点,
中点,![]() 且
且![]() ,设三棱锥
,设三棱锥![]() 的体积为
的体积为![]() ,三棱锥
,三棱锥![]() 与三棱锥
与三棱锥![]() 的公共部分的体积为
的公共部分的体积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,直线
,直线![]() 与
与![]() 轴交点为
轴交点为![]() ,与
,与![]() 的交点为
的交点为![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)过![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,若
两点,若![]() 的垂直平分线
的垂直平分线![]() 与
与![]() 相交于
相交于![]() 两点,且
两点,且![]() 四点在同一圆上,求
四点在同一圆上,求![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com