
【题目】![]() 是个循环小数,
是个循环小数,![]() 表示
表示![]() 的小数点后第
的小数点后第![]() 位开始,连续
位开始,连续![]() 位上的数字之积.证明存在自然数
位上的数字之积.证明存在自然数![]() 、
、![]() ,对任意的
,对任意的![]() 、
、![]() ,均有
,均有![]() .
.
科目:高中数学 来源: 题型:
【题目】已知![]() ,将函数
,将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度后,得到函数
个单位长度后,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的表达式;
的表达式;
(2)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(3)若函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某村充分利用自身资源,大力发展养殖业以增加收入.计划共投入80万元,全部用于甲、乙两个项目,要求每个项目至少要投入20万元在对市场进行调研时发现甲项目的收益![]() 与投入x(单位:万元)满足
与投入x(单位:万元)满足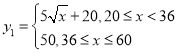 ,乙项目的收益
,乙项目的收益![]() 与投入x(单位:万元)满足
与投入x(单位:万元)满足![]() .
.
(1)当甲项日的投入为25万元时,求甲、乙两个项目的总收益;
(2)问甲、乙两个项目各投入多少万元时,总收益最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com