
���� ��I��������֪��ԲC��ֱ������ϵ���̣��ɵ�ԲC�ļ����귽�̣�
����ֱ��l�IJ����������εõ�ֱ��l����ͨ���̣������ɵ�ֱ��l�ļ����귽��
������֪����OM��ԲC�Ľ���ΪO��P������=$\frac{3��}{4}$���ͣ��ɵ�P��Q��ļ����꣬�����õ��߶�PQ�ij���
��� �⣺��I����ԲC��ֱ������ϵ����Ϊx2+y2+2x-2y=0��
��ԲC�ļ����귽��Ϊ����2+2��cos��-2��sin��=0��
����+2cos��-2sin��=0��
��${��}^{\;}=2\sqrt{2}sin����-\frac{��}{4}��$��
��ֱ��l�IJ�������Ϊ$\left\{\begin{array}{l}{x=-1+t}\\{y=t}\end{array}\right.$��tΪ��������
���εã�x-y+1=0��
��ֱ��l�ļ����귽��Ϊ����cos��-��sin��+1=0��
��sin��-cos��=$\frac{1}{��}$��
������=$\frac{3��}{4}$ʱ��|OP|=$2\sqrt{2}sin��\frac{3��}{4}-\frac{��}{4}��$=2$\sqrt{2}$��
�ʵ�P�ļ�����Ϊ��2$\sqrt{2}$��$\frac{3��}{4}$����
|OQ|=$\frac{1}{\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}}$=$\frac{\sqrt{2}}{2}$��
�ʵ�Q�ļ�����Ϊ��$\frac{\sqrt{2}}{2}$��$\frac{3��}{4}$����
���߶�PQ�ij�Ϊ��$\frac{3\sqrt{2}}{2}$��
���� ���⿼���֪ʶ���Dz������̺ͼ����꣬�������ղ�����������ͨ���̼������귽��֮���ת����ʽ���ǽ��Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{��}{2}$ | B�� | $\frac{��}{2}$ | C�� | 1 | D�� | -1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
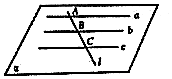
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 8 | C�� | 11 | D�� | 18 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
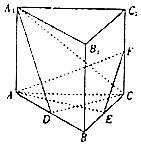 ��ͼ������������ABC-A1B1C1�У�E��F�ֱ���BC��CC1���е㣮
��ͼ������������ABC-A1B1C1�У�E��F�ֱ���BC��CC1���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������P-ABCD�ĵ���ABCD�������Σ�PA�͵���ABCD��PA=AD��E��F�ֱ�����PD��BC���е㣮
��ͼ������P-ABCD�ĵ���ABCD�������Σ�PA�͵���ABCD��PA=AD��E��F�ֱ�����PD��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2$\sqrt{2}$i | B�� | 2$\sqrt{2}$ | C�� | ��2$\sqrt{2}$i | D�� | ��2$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com